能量法(energy method)又稱能量原理。在固體力學中,把功與能量相關的一些原理和方法統稱為能量法,具體有互等原理、卡式原理、虛功原理、單位載荷法及摩爾積分法等等。
其對結構的變形計算及超靜定結構的求解起著重要的作用,特別是近些年來隨著計算力學的興起,使得能量法更加受到重視。
基本介紹
- 中文名:能量法
- 外文名:energy method
- 解決問題:構建變形,超靜定解構
- 套用領域:固體力學,靜力學
- 別名:能量原理
應變能



















常用的能量法
互等定理



















卡氏定理








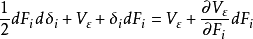


虛功原理





單位載荷法








摩爾積分法


能量法(energy method)又稱能量原理。在固體力學中,把功與能量相關的一些原理和方法統稱為能量法,具體有互等原理、卡式原理、虛功原理、單位載荷法及摩爾積分法等等。
其對結構的變形計算及超靜定結構的求解起著重要的作用,特別是近些年來隨著計算力學的興起,使得能量法更加受到重視。














































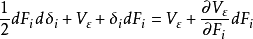

















能量法(energy method)又稱能量原理。在固體力學中,把功與能量相關的一些原理和方法統稱為能量法,具體有互等原理、卡式原理、虛功原理、單位載荷法及摩爾積分法...
《強非線性系統周期解的能量法》是2008年5月1日科學出版社出版的圖書。本書研究強非線性系統周期解的新的分析方法——能量法。...
內容簡介本書共分六個部分.討論的方法有:隔離體法、能量方法,守恆方法,類比方法、組合方法,選系方法、參考系變換法,演繹方法、統計方法、對稱方法、力線方法、特...
相機上的接受器接受反射回來的紅外光或超音波進行對焦,其光學原理類似三角測距對焦法.主動式中又有能量法,用於低檔普及型相機的自動對焦,廣泛用於各種平視取景相機....
上限法,也稱能量法,屬於極限分析法。極限分析法基於虛功原理和變分極值原理,用於尋求複雜塑性成形問題的近似解。上限法只考慮動而不考慮靜,故只滿足動而未必滿足靜...
靈氣療法就是一種利用宇宙能量進行治病、養生、修煉的方法,是目前世界自然醫學領域中公認的最簡捷、最高效、最方便、最優秀的能量療法體系。...
9.2.2 能量法……1919.2.3 非彈性穩定性……1939.3 連續壓桿的穩定性計算……1959.3.1 在剛性支座上連續壓桿的穩定性……195...
改革的經驗和理論力學與材料力學這兩門課程所研究的力的兩方面效應——運動效應和變形效應,,對其本質上一致的地方和不同之處以平衡法和能量法(拉格朗日力學)作為兩...
——矢量方法、點的運動和剛體基本運動、點的合成運動、剛體的平面運動、質點動力學、質點系動力學——矢量方法、平衡問題——能量方法、質點系動力學——能量方法...
最後,討論了半線性波動方程的整體適定性問題以及研究方法,其中包括具有整體Lipschitz非線性項的波動方程的整體解;半線性波動方程的有限能量弱解、經典解以及三個空間...
