基本介紹
- 中文名:約化密度矩陣
- 外文名:Reduced density matrix
- 領域:量子力學
密度矩陣


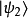
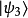
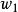
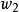
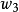


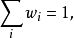
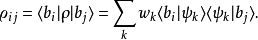
約化密度算符

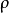
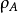
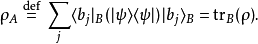

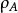
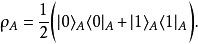

參閱
- 玻恩法則(Born rule)
- 葛利生定理(Gleason's theorem)


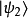
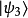
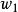
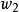
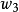


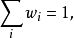
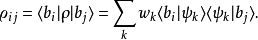

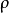
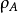
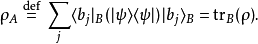

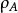
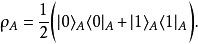

在量子力學裡,密度算符(density operator)與其對應的密度矩陣(density matrix)專門描述混合態量子系統的物理性質。約化密度算符的點子最先由保羅·狄拉克於1930年...
自洽場理論;③分子軌道對稱守恆理論;④李群、李代數和量子化學中的多體問題;⑤二階約化密度矩陣理論;⑥高分子固化理論和標度研究等。這些課題的研究成果,先後在...
自然空間自旋軌道,即一階約化密度矩陣ρ1的正交歸一的本徵函式,占據數就是其本徵值。占據數接近l的自然軌道稱為主自然軌道,占據數很小者稱為相關自然軌道。...
《數位化量子力學》內容簡介:《數位化量子力學》是作者精心為廣大讀者朋友們編寫...12.1.3 複合體系的密度矩陣與子系的約化密度矩陣 12.1.4 用約化密度矩陣...
在此基礎上依次介紹密度矩陣、相對論性波動方程、路徑積分、二次量子化方法、量子場理論、電磁場的量子效應和量子散射理論。其中的量子場理論部分,主要講述正則量子化...
3、約化密度矩陣理論;4、溶劑效應;5、數值計算方法。陳飛武主要貢獻 編輯 學術論著:1. 陳飛武,量子化學中的計算方法,科學出版社,北京,2008年6月....
此類測量結果均是可分離的,只和兩個約化密度矩陣及有關。iii)聯合測量 :測量不是局域進行的,類似於下面不可分離類型的力學量測量此類測量結果均不是可分離的,和...
第14章介紹電子相關問題,第15章介紹密度泛函理論方法,第16章介紹有效芯勢方法。...14.4 約化密度矩陣和自然軌道 14.4.1 約化密度矩陣 14.4.2 CI波函式的密...
1.2密度矩陣1.2.1密度算符與密度矩陣1.2.2混合態的密度矩陣1.2.3複合體系的子體系,約化密度矩陣1.2.4波函式統計詮釋的進一步理解...
約化密度矩陣的對角元素有效消失所需的時間稱為退相干時間。對於日常發生的巨觀過程,退相干時間非常短暫。特別而言,在物理學者給出的很多不同的退相干模型里,不同...
全書共8章。具體內容包括數學預備知識,量子力學導論,Hartree-Fock方程及自洽場計算,單電子和雙電子積分計算,組態相互作用計算,微擾理論,耦合簇理論和約化密度矩陣理論...
1.3.2約化密度矩陣 1.3.3 Schmidt分解,von Neumann熵 1.3.4波函式統計詮釋的一種觀點 第2章量子力學與經典力學的關係 2.1對應原理 2.2 Poisson括...
高分子反應統計理論》、《量子化學》、《套用量子化學》、《約化密度矩陣引論》 [5] 人物生平 主要成就 科學研究 主要論著 人才培養 ...
離子液體物理化學性質的研究也能為離子液體結構的研究及新型功能化的離子液體的...4.4.1 閉殼層體系一級和二級約化密度矩陣表達式 4.4.2 能量表達式 4.4.3 變...
是約化密度矩陣的第 個本徵值。 [1] 糾纏譜糾纏熵 編輯 一個由A部分和B部分組成的量子力學的系統,A與B之間可能存在某種遠距離的相關性,即使A與B之間並不存...
第三章詳述了輸運理論及計算方法,其中包括主房程、散射矩陣、格林函式和約化密度矩陣法,最後提出我們認為最有效的計算辦法。第四章以我們進來的工作作為套用篇結尾...
群論基礎、群論套用、分子光譜、電子相關、價鍵理論、密度泛函理論以及量子化學...密度矩陣方法228密度函式2282密度算符2283約化密度矩陣229及相關模型230...
