有關公式
W有用
W總
W額外
專業名詞解釋
簡單機械
凡能夠改變力的大小和方向的裝置,統稱“機械”。利用機械既可減輕體力勞動,又能提高工作效率。機械的種類繁多,而且比較複雜。根據
伽利略的提示,人們曾嘗試將一切機械都分解為幾種簡單機械,實際上這是很困難的,通常是把以下幾種機械作為基礎來研究。例如,
槓桿、
滑輪、
輪軸、齒輪、斜面、螺旋、劈等。前四種簡單機械是槓桿的變形,所以稱為“槓桿類簡單機械”。後三種是斜面的變形,故稱為“斜面類簡單機械”。不論使用哪一類簡單機械都必須遵循機械的一般規律——功的原理。
槓桿
用剛性材料製成的形狀是直的或彎曲的桿,在外力作用下能繞固定點或一定的軸線轉動的一種簡單機械。其上有
支點(用O表示),動力(F)作用點,阻力(W)作用點,槓桿的固定轉軸就是通常所說的“支點”,從轉軸到動力
作用線的垂直距離叫“
動力臂”,從轉軸到阻力作用線的垂直距離叫“
阻力臂”。上述就是通常所講的三點兩臂。由於槓桿上三點的位置不同,即產生不同的受力效果。
槓桿原理
F1· L1=F2·L2式中,F1表示動力,L1表示
動力臂,F2表示
阻力,L2表示
阻力臂。從上式可看出,欲使槓桿達到平衡,
動力臂是
阻力臂的幾倍,動力就是阻力的幾分之一。在使用槓桿時,為了省力,就應該用動力臂比
阻力臂長的槓桿;如欲省距離,就應該用
動力臂比阻力臂短的槓桿。因此使用槓桿可以省力,也可以省距離。但是,要想省力,就必須多移動距離;要想少移動距離,就必須多費些力。要想又省力而又少移動距離,是不可能實現的。
 簡單機械
簡單機械動力
任何機械,不論是簡單的還是複雜的,在工作時,總要受到兩種力的作用:一種是推動機械的力叫作“動力”動力是使槓桿轉動的力。另一種是阻礙機械運動的力叫作“
阻力”,阻力是阻礙槓桿轉動的力。動力可以是人力,也可以是畜力、
風力、電力、水力、蒸汽壓力等,阻力除了我們要克服的有用阻力之外,還有一些是不可避免的無用阻力。
作用線
通過力的作用點沿力的方向所引的直線,叫作“力的作用線”。
動力臂
從支點到力的
作用線的垂直距離叫“力距”。從
支點到動力F1的作用線的垂直距離L1叫作“
動力臂”;從支點到阻力F2的作用線的垂直距離L2叫作“
阻力臂”。如果把從動力點到
支點的棒長距離作為
動力臂,或把從阻力點到支點的棒長距離作為
阻力臂,這種認識是錯誤的。這是因為對
動力臂和
阻力臂的概念認識不清所致。
阻力臂
見動力臂條。
轉動軸
轉動是常見的一種運動。當物體轉動時,它的各點都做
圓周運動,這些圓周的中心在同一直線上,這條直線叫做“轉動軸”。門、窗、砂輪、電動機的轉子等都有固定轉軸,只能發生轉動,而不能平動。幾個力作用在物體上,它們對物體的轉動作用決定於它們的
力矩的代數和。若
力矩的代數和等於零,物體將用原來的
角速度做勻速轉動或保持靜止。
三類槓桿
對槓桿的分類一般是兩種方法。第一種是以
支點、阻力點和動力點所處的位置來分的;另一種是按省力或費力來區分的。無論怎樣來劃分,總離不開省力、費力、等臂這幾種情況。
 簡單機械
簡單機械名稱 | 結構特徵 | 特點 | 套用舉例 |
省力槓桿 | 動力臂大於阻力臂(L1>L2,F1<F2) | 省力、費距離 | 撬棒、鍘刀、動滑輪、輪軸、羊角錘、鋼絲鉗、手推車、花枝剪刀 |
費力槓桿 | 動力臂小於阻力臂(L1<L2,F1>F2) | 費力、省距離 | 縫紉機踏板、起重臂、人的前臂、理髮剪刀、釣魚桿、鑷子、船槳 |
等臂槓桿 | 動力臂等於阻力臂(L1=L2,F1=F2) | 不省力、不費力 | 天平、定滑輪 |
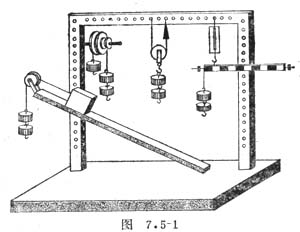
機械效率
表示機械省力程度的物理量。機械雖然絕對不能省功,但可以省力。使機械作功的力稱為“動力”(F),阻礙機械作功的力稱為“
阻力”(P)。使用機械的目的,在於使用很小的動力而與
阻力平衡。所謂機械效率(A),就是機械的有用阻力(P)跟動力(F)的比值。
機械效率<1時,省力費時,例如,
獨輪車、鉗子、起子、省力的槓桿等都是省力的機械。
機械效率=1時,不省力,也不費力。例如物理天枰。機械效率<1時,也可能費力省時,例如竹夾、火鉗等。機械利益是由實際測得的有用阻力和動力的大小所決定。由於機械潤滑情況的不同,在克服同樣的有用阻力時,亦有所不同。機械潤滑得不好,無用阻力大,需要動力也大,
機械效率就小些;機械潤滑得好,無用阻力小,需要的動力也小,機械效率就大些。新生產出的機器需要磨合,汽車出廠要用上一段時間,目的是使其
摩擦阻力減小。但機器陳舊,機件磨損,又會增加阻力。
槓桿的套用
不同類型槓桿各具有不同的特點和用途。掌握了
槓桿原理,就可根據需要有意識地選用不同類型的槓桿來使用。應明確:
省力槓桿省力但要多移動距離,
費力槓桿費力但省距離,
等臂槓桿不省力也不省距離,又省力又省距離的槓桿是沒有的。有的槓桿是否省力或省距離,不是永恆不變的。根據使用情況的不同,會由省力變為省距離。例如,用鐵鍬鏟土,往車上裝土的過程都會有所改變。鏟土時
支點在動力點及阻力點之間,在裝土時動力點在支點與阻力點之間。為此,在使用槓桿時應注意幾點:
1.解答槓桿問題時,必須根據題意畫出示意圖,在圖上標出槓桿的支點、動力
作用線和阻力作用線。同時用
線段標明
動力臂和
阻力臂的大小,再根據
槓桿平衡條件,列出方程,進行計算。
2.
力臂是一個重要的概念。力臂是從
支點到力的作用線的垂直距離,不要理解為
力臂是從支點到力的作用點的長度。動力和阻力都是指作用在同一槓桿上的力,而不是作用在重物或其他物體上的力。
3.畫槓桿示意圖的方法:
(1)畫出槓桿:用粗直線表示直槓桿,用變曲的粗線表示曲槓桿。
(2)在槓桿轉動時找出
支點,並在支點旁用箭頭表示槓桿轉動的方向。
(3)根據轉動方向判斷動力、阻力的方向。動力、阻力的作用點應畫在槓桿上,可用力的示意圖表示。
4.
槓桿的平衡條件,適用於任意一個
平衡位置上,所謂槓桿的平衡是指槓桿靜止不轉動或勻速轉動。
桿秤
它是測量物體質量的量度工具,是以提紐為轉動軸,根據槓桿平衡原理製造的。桿秤主要由
秤桿、秤砣、秤鉤(或秤盤)等構成。如圖1-23所示。G表示桿秤的重力,B點是它的重點,未掛重物時若將
A點即為桿秤的“定盤星”。在秤鉤上加物W後,將秤砣從A點移到A'
力G相對應的刻度A'的位置。桿秤是我國勞動人民所發明並使用已久的測量工具,舊秤以斤,兩為單位計量,現代則以以千克計量。
力矩
又叫“轉矩”,是表示力對物體作用時,使物體發生轉動或改變轉動狀態的物理量。力矩是
矢量。力矩的大小等於力與從轉軸到力的
作用線的垂直距離之乘積。如果物體所受的力不在垂直於轉軸O的平面內,就必須把力分解成兩個
分力:一個
分力與轉軸平行;另一個分力是在轉動的平面內。只有轉動平面內的
分力才可能改變物體的轉動狀態。因此,在力矩等於力跟
力臂乘積的計算中,應理解力是在它的作用點的轉動平面內的分力。如這一點在力的作用線上,則力矩為零。如果若干個力同時作用在一個物體上,則合力矩是所有分力矩的代數和。一個處於平衡的物體,順時針方向力矩的和等於逆時針方向力矩的和,在
國際單位制中,力矩的單位是米·
牛頓。其方向用
右手螺旋法則決定。在中學階段,因為只研究有固定轉軸的物體的平衡,力矩就只有兩種轉向。規定物體逆時針轉動的力矩為正,使物體順時針轉動的力矩為負。力矩愈大,使物體轉動狀態發生改變的效果就愈明顯。用大小相同的力推門時,力的作用點離轉軸愈遠,且方向垂直於門,
力臂愈大,則推門愈省力。
力偶
大小相等、方向相反,但作用線不在同一直線上的兩個力叫作“
力偶”。用雙手攻螺紋或用手旋鑰匙、水龍頭時,所施加的作用常是力偶。它能使物體發生轉動,或改變其轉動狀態。汽車駕駛員雙手轉動轉向盤時所施加的一對力就是一個力偶。力偶的轉動效果決定於
力偶矩的大小。
力偶矩等於其中任何一個力的大小和兩力
作用線之間的垂直距離(
力偶臂)的乘積。如圖1-24所示。如果作用力F的方向跟AB垂直,AB的長度等於d,那么這個力偶的
力偶矩(M)為:
M=±Fd。
式中Fd為
力偶矩的大小,符號用來表示力偶的轉向。規定
力偶逆時針轉向取“+”,反之取“-”(也可規定,力偶順時針轉向取“+”,那么力偶逆時針轉向就取“-”)。應注意:
力偶中力的方向不跟AB垂直時,應像
力矩那樣分解成垂直分量,再進行計算。力偶的
轉矩(即
力偶矩)和所繞著轉動的點無關。由於
力偶的
合力為零,它不能使物體產生
位移,只能使物體發生轉動或改變物體的轉動狀態。
力偶矩
簡稱為“力偶的力矩”,亦稱“力偶的轉矩”。
力偶是兩個相等的
平行力,它們的合力矩等於平行力中的一個力與平行力之間距離(稱
力偶臂)的乘積,稱作“
力偶矩”,力偶矩與
轉動軸的位置無關。
力偶矩是
矢量,其方向和組成力偶的兩個力的方向間的關係,遵從右手螺旋法則。對於有固定軸的物體,在
力偶的作用下,物體將繞固定軸轉動;沒有固定軸的物體,在力偶的作用下物體將繞通過質心的軸轉動。
力偶臂
力偶之兩個力之間的垂直距離。見
力偶條圖1-24所示。
輪軸
是固定在同一根軸上的兩個半徑不同的輪子構成的槓桿類簡單機械。
半徑較大者是輪,半徑較小的是軸。從形式上看是圓盤,但從實質上看起來只有它們的直徑或
半徑起力學作用。用R表示輪
半徑,也就是
動力臂;r表示軸半徑,也就是
阻力臂;O表示支點。當輪軸在作勻速轉動時,動力×輪半徑=阻力×軸半徑,所以輪和軸的半徑相差越大則越省力。上式動力用F表示,阻力用W表示,則可寫成FR=Wr。
即利用輪軸可以省力。若將重物掛在輪上則變成費力的輪軸,但它可省距離。輪軸的原理也可用機械功的原理來分析。輪軸每轉一周,動力功等於F×2πR,阻力功等於W×2πr。在不計無用阻力時,機械的
日常生活中常見的轆轤、絞盤、石磨、汽車的駕駛盤、手搖卷揚機等都是輪軸類機械。
滑輪
滑輪是屬於槓桿變形的一種簡單機械,是可以繞中心軸轉動的,周圍有槽的輪子。使用時,根據需要選擇。滑輪可分為
定滑輪、
動滑輪、
滑輪組、
差動滑輪等。有的省力,有的可以改變作用力的方向,但是都不能省功。
定滑輪
滑輪的軸固定不動,它實質上是一個等臂槓桿。動力臂和
阻力臂都是滑輪的半徑r,根據
槓桿原理Fr1=Wr2。它的機械利益為
變了動力的方向,如要把物體提到高處,本套用向上的力,如利用
定滑輪,就可以改用向下的力,因而便於工作。
動滑輪
滑輪的軸和重物一起移動的滑輪。它實質上是一個
動力臂二倍於
阻力臂的槓桿。根據
槓桿平衡的原理Wr=F·2r,它的機械利
改變用力的方向。其方向是與物體移動的方向一致。
滑輪組
動滑輪和
定滑輪組合在一起叫“滑輪組”。因為
動滑輪能夠省力,
定滑輪能改變力的方向,若將幾個動滑輪和
定滑輪搭配合併而成滑輪組,既可以改變力的大小,又能改變力的方向。普通的滑輪組是由數目相等的
定滑輪和
動滑輪組成的。而這些滑輪或者是上下相間地坐落在同一個輪架(或叫“輪轅”),或者是左右相鄰地裝在同一根軸心上。繩子的一端固定在上輪架上,即相當於系在一個固定的吊掛設備上,然後依次將繩子繞過每一個下面的
動滑輪和上面的
定滑輪。在繩子不受拘束的一端以F力拉之,被拉重物掛在活動的輪架上。對所有各段繩子可視為是
互相平行的,當拉力與重物平衡時,則重物W必平均由每段繩子所承擔。若有n個定滑輪和n個
動滑輪時,
且為勻速運動時,則所需之F力的大小仍和上面一樣。因此,在提升重物時才能省力。其傳動比乃為F∶W=1∶2n。注意,在使用滑輪組時,不能省功,只能省力,但省力是以多耗距離(即行程)為前題的。
前邊所分析的定滑輪、
動滑輪以及滑輪組,都是在不計滑輪重力,滑輪與軸之間的
摩擦阻力的情況下得出的結論。但在使用時,實際存在輪重和摩擦阻力,所以實際用的力要大些。
差動滑輪
即鏈式升降機,是一種用於起重的滑輪組。上面是由兩個直徑不同裝在同一個軸上的圓盤A、B組成的
定滑輪。下面是一個
動滑輪,用鐵索與上面的
定滑輪聯結起來而成滑輪組。若大輪A的半徑是R,小輪B的半徑是r,如圖所示。當動力F拉鏈條使大輪轉一周,動力F拉鏈條向下移動了2πR,大輪捲起鏈條2πR,此時小輪也轉動一周,並放下鏈條長2πr於是
動滑輪和重物W上升的高度為2π(R-r)。
 差動滑輪
差動滑輪由於2R大於(R-r),
差動滑輪的機械利益大於1,若提高機械利益,可加大兩輪的半徑同時縮小兩輪間的半徑差。這種機械,亦稱“神仙葫蘆”,有手動,也有用電來驅動的。鏈條是閉合的,為防止
滑輪和鏈條間的滑動,滑輪上有齒牙與鏈條配合運動。
斜面
簡單機械的一種,可用於克服垂直提升重物之困難。距離比和力比都取決於傾角。如
摩擦力很小,則可達到很高的效率。用F表示力,L表示斜面長,h表示斜面高,
物重為G。不計無用
阻力時,根據功的原理。得
 簡單機械
簡單機械FL=Gh。實驗證明,沿著光滑斜面向上拉重物所需要的拉力F小於重物的所受的重力G,即利用斜面可以省力,當斜面高度一定時,長度L不同的斜面所需的拉力也不同:L越長,F越小,越省力
傾角越小,斜面越長則越省力,但費距離。
螺旋
屬於斜面一類的簡單機械。例如螺旋千斤頂可將重物頂起,它是省力的機械。千斤頂是由一個陽螺旋桿在陰螺旋管里轉動上升而將重物頂起。根據功的原理,在動力F作用下將螺桿旋轉一周,F對螺旋做的功為F2πL。螺旋轉一周,重物被舉高一個螺距(即兩螺紋間豎直距離),螺旋對重物做的功是Gh。依據功的原理得
很小的力,就能將重物舉起。螺旋因摩擦力的緣故,效率很低。即使如此,其力比G/F仍很高,距離比由2πL/h確定。螺旋的用途一般可分緊固、傳力及傳動三類。
齒輪和齒輪組
兩個相互咬合的齒輪,在它們處於平衡狀態時,不省力,因為齒輪的實質是兩個等臂槓桿,所以咬合的齒輪不省力,只省圈數。
劈
亦稱“尖劈”,俗稱“楔子”。它是簡單機械之一,其截面是一個三角形(
等腰三角形或直角三角形)。三角形的底稱作劈背,其他兩邊叫劈刃。施力F於劈背,則作用於被劈物體上的力由劈刃分解為兩部分,P是加在劈上的阻力,如果忽略劈和物體之間的摩擦力,利用
力的分解法,知P與劈的斜面垂直,P的作用可分成兩個
分力:一個是與劈的
運動方向垂直,它的大小等於P·cosα,對運動並無影響;另一個是與劈的運動方向相反的,它的大小等於P·sinα,對運動起
阻礙作用。所以,當F=2P·sinα時劈才能前進,因而P與F大小之比等於劈面的長度和劈背的厚度之比,因此劈背愈薄,劈面愈長,就愈省力。劈的用途很多,可用來做切削工具,如刀、斧、刨、鑿、鏟等;可用它緊固物體,如鞋楦榫頭,斧柄等加楔子使之漲緊;還可用來起重,如修房時換柱起梁等。
功
是描述物體狀態改變過程的物理量,能量變化的量度。功的概念來源於日常生活中的“工作”一詞。在
物理學中,它有特殊的含義。當物體在
恆力F的作用下,力的作用點的
位移是S時,這個功就等於力跟距離的乘積。對國中學生來說,只要明確“在力的作用下,物體沿力的方向通過了一段距離,那么這個力就對物體做了功”,這是指物體在
恆力作用下,沿力的方向作單向
直線運動的情況,所以對功的計算可用公式W=FS。當物體在
恆力作用下,作非單向直線運動,如
豎直上拋運動、
平拋運動、
斜拋運動等等,物體受力方向和
運動方向不一定是一致時,對功的理解應加深為“力對物體所做的功,等於力的大小、力的作用點的
位移大小,力和位移間夾角的餘弦三者之乘積”即W=FScosα。式中W表示
外力F對物體所做的功,S表示物體移動的路程,α表示F與S之間的夾角。根據
公式研究力對物體
做功的一些情況:
2.當0°<α<90°時,1>cosα>0,則力F的有效分力Fcosα和物體的
運動方向一致,力F對物體做
正功;
3.當α=90°時,cosα=0,則W=0,此時力F對物體不
做功;
4.當180°>α>90°時,-1<cosα<0,則W<0,即W為負值。在這種情況下F對物體做
負功,也可說成物體克服
阻力F做功;
5.當α=180°時,則W=-FS,這時力F對物體做
負功,或者說成物體克服
阻力F做功。
必須注意:在研究有關“功”的問題時,應分清有沒有
做功,誰在做功。功是一個只有大小而沒有方向的
物理量,它是標量而不是矢量。至於正功和
負功,不過是區別外力對物體
做功還是物體克服阻力做功,或用來表示力與路程同向還是反向,並不是功有方向性。
功是力對空間的累積效應。力對物體
做功,使物體發生位置或
運動狀態的改變,因而也就發生了
機械能的改變。功即是反映在這一過程中,物體
機械能改變多少的物理量。在力學中功的狹義概念僅指機械能轉換的量度;而在
物理學中功的廣義概念指除
熱傳遞外的一切能量轉換的量度。所以功也可定義為能量轉換的量度。一個系統總
能量的變化,常以系統對外做功的多少來量度。
能量可以是機械能、
電能、
熱能、
化學能等各種形式,也可以多種形式的能量同時發生轉化。功的單位和
能量單位一樣,在
國際單位制中,都是焦耳。
計算變力做功是把運動的軌跡分成許許多多無限小的小段,在每個小段內,可以把力看作為恆力,按恆力做功的定義來計算在各個小段內所做的功,最後把各個小段的功加起來,就是變力做的功,即A=ΣFi·ΔSi,如果力和位移都是連續的,則可用積分法計算,
功的原理
亦稱“機械功的原理”。即動力對機械所做的功等於機械克服
阻力所做的功。也就是說利用任何機械都不能省功。動力功W動,又稱輸入功或
總功。
阻力功W阻,包括克服有用阻力所做的W有用(又稱輸出功)和克服無用阻力所做的W無用(又稱損失功),即W動=W阻=W有用+W無用。也可寫成W輸入=W輸出+W損失。功的原理是機械的基本原理。要省力就要多移動距離,要少移動距離就要多用力,使用任何機械都不能省功。在機械
做功過程中,只有在不存在無用阻力,機械本身作
勻速運動的理想情況下,
有用功才等於
總功,效率為100%。事實上,必然存在無用阻力,效率一定小於100%,也就是說使用任何機械,在實際情況下總是費功的。應明確,只有在理想情況下,
有用功才等於
總功。
正功
作用力的方向和力的作用點的位移方向之夾角小於90°且大於或等於0°時(即α為銳角),根據公式作用力A做正功。當力F與位移S夾角α=0°時,W=FScos0°=FS,F做最大正功;0°<α<
負功
當作用力方向與力的作用點位移方向夾角大於90°且小於或等於180°時,這時cosα<0,根據公式功為負。力對物體作負功-A就代表受力作用的物體克服阻力作了正功A。這兩種說法描述的是同一物理過程。例如,空氣壓縮機中空氣對活塞作負功,也可以說成是活塞克服空氣的壓力作正功。又如,汽車緊急制動,車輪停止轉動,輪胎在地面上滑動,這時
摩擦力對汽車作負功,反過來也可以說汽車克服摩擦力作正功。
功率
功跟完成這些功所用時間的比值叫做“功率”。最初定義功率為“單位時間裡完成的功”,它是指
做功快慢不變的情況,國中學生易於掌握。“功跟完成這些功所用時間的比值”這一定義功率,對於
做功快慢不變的情況,既表示平均功率,又表示
即時功率。對於
做功快慢不均勻的情況,如時間取得長些,則為平均功率;時間趨於零,這一
率,只能表示機器在一段時間t內的
平均功率。而由
公式P=Fv計算出來的功率就有了不同的含義。若速度v代表平均速度,那么P代表
平均功率,如果v代表即時速度,那么P就代表機器在某瞬時的
即時功率。
公式中力是一個
矢量,速度也是一個矢量,而功率卻是一個標量。
方法,一為“
標積”;一為“矢積”。兩
矢量的“
標積”為一標量,其大小(к)為兩矢量的大小和兩矢量夾角的餘弦的乘積,用公式表示為
式P=Fv中,實際上P應為 矢量和 矢量的
標積,即
所以得到的功率P應為一標量。
關於
公式P=Fv,中F與v成反比的關係,應明確,不能脫離具體條件,防止得出謬誤的結果。因為機器的牽引力要受速度的限制,又受機器的構造、運轉條件等限制,任何機器在設計製造時,已規定了它的正常功率和最大作用力。超過最大作用力範圍,牽引力和速度成反比這一關係就不能適用。另一方面也不能使機器的牽引力趨近於零,而使機器的速度無限制地增加。因為任何機器在工作時要受到
阻力作用,阻力還與機器運轉的速度有關。即使在沒有負載的情況下,機件間的
摩擦阻力仍然存在。為維持機器的運轉,發動機的牽引力不能小於它所受的阻力。因而它的速度也不能無限增加。因此,任何機械在有一定的
最大輸出功率的同時,還具有一定的最大速度和最大作用力。
功率的常用單位是
瓦特(焦耳/秒),簡稱瓦,單位符號W。瓦特這個單位較小,技術上常用千瓦做功率的單位。過去還有爾格/秒、牛頓·米/秒、千克力·米/秒。
間t內的平均功率。當物體受
恆力作用時也可表示為P=F 。式中 表示某段時間的平均速度。平均功率隨所取的時間不同而不同,因此在談到平均功率時,一定要指出是哪一段時間內的平均功率。參閱功率條。
即時功率
即“瞬時功率”,簡稱功率。描述機械在某一瞬間作
物體運動即時速度的乘積。作平均速度時,P當然代表
平均功率,如果作即時速度,那么P就代表機械在某瞬時的
即時功率。當作
勻速運動時,即時功率和平均功率相同
槓桿概念:當動力點離
支點的距離小於阻力點離支點的距離時,省力。
當動力點離支點的距離大於阻力點離支點的距離時,費力。
當動力點離
支點的距離等於阻力點離支點的距離時,不省力也不費力。
分類法
第一種分類法
第一類槓桿:是動力F和有用阻力W分別在支點的兩邊。這類槓桿
不省力也不費力。例如,剪金屬片用的剪刀,刀口很短,它的機械利益遠大於1 。這是因為金屬板很硬,刀口短,刀把長,即
動力臂大於
阻力臂,可以少用力。屬於這種情況的槓桿還有克絲鉗等。家庭裁衣剪布用的剪刀,把與刃基本是等長的,即
動力臂等於
阻力臂,屬於不省力也不費力的類型。因為布的厚度較薄,不需太大的力,剪布要直故刀口要長些,為此用力不大,布剪的也直。屬於這種類型的還有
物理天平。又如理髮用的剪刀,刀口很長,即
動力臂小於
阻力臂,它的機械利益小於1。這是因為剪髮本來不需要多大的力,刀口長一些,能夠剪得快一些和齊一些。
第二類槓桿:是支點和動力點分別在有用阻力點的兩邊。這類槓桿的
動力臂大於
阻力臂,其機械利益總是大於1,所以總是省力的。例如,用鍘刀鍘草、獨輪車等都是這類槓桿。
第三類槓桿:是
支點和有用阻力點分別在動力點的兩邊,這類槓桿的
動力臂小於
阻力臂,其機械利益總是小於1,所以總是費力的。例如,縫紉機的腳踏板、夾食品的竹夾子都屬於這類槓桿。
第二種分類法
第一類槓桿:是省力的槓桿,即動力臂大於阻力臂。例如,羊角錘、木工鉗、獨輪車、汽水板子、鍘刀等等。
第二類槓桿:是費力的槓桿,即
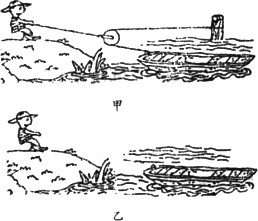
動力臂小於阻力臂。如鑷子、釣魚桿、理髮用的剪刀。
第三類槓桿:不省力也不費力的槓桿,即
動力臂等於阻力臂。其機械利益等於1。如天平、
定滑輪等。










 簡單機械
簡單機械 簡單機械
簡單機械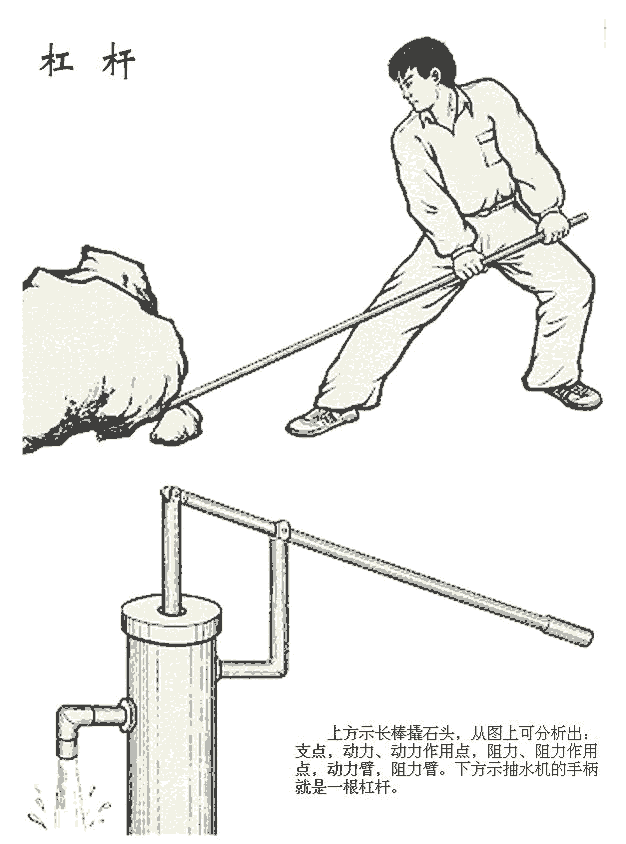
 差動滑輪
差動滑輪 簡單機械
簡單機械