基本介紹
- 中文名:簡化模型
- 外文名:Simplified Model
- 學科:自動化、計算機科學
- 定義:減少模型的複雜度
- 目的:更容易分析
- 方法:降維、聚類、改變參數的條件
- 套用:大系統、汽車、地震等
概述
大系統理論
內容
特點
簡化模型技術
頻域簡化
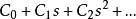

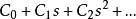
簡化模型(simplified model),也可以稱之為模型簡化,簡單來說是指去掉模型中不顯著的項,通過減少項數使模型更容易使用,或者是指減少模型的複雜度,使模型更容易計算...
大規模系統模型簡化(model simplification forlarge scale system)尋找一個簡單的數學模型以代替原有的大規模系統模型的方法.簡化模型必須保留原系統的某些主要動態特性...
在機率統計理論中, 生成模型是指能夠隨機生成觀測數據的模型,尤其是在給定某些隱含參數的條件下。它給觀測值和標註數據序列指定一個聯合機率分布。在機器學習中,生成...
又稱簡約眼或模型眼,是一種簡化眼的折光系統而成像的模型眼。為李斯丁(Listing)首先提出。鑒於眼的折光系統太複雜,由角膜、房水、晶狀體及玻璃體等組成,而這些...
簡化生物圈模型編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!中文名稱 簡化生物圈模型 英文名稱 simplified biosphere...
通過主觀意識藉助實體或者虛擬表現構成客觀闡述形態結構的一種表達目的的物件(物件並不等於物體,不局限於實體與虛擬、不限於平面與立體)。模型≠商品。任何物件定義為...
理想模型是為了便於研究而建立的一種高度抽象的理想客體。實際的物體都是具有多種屬性的,例如固體具有一定的形狀、體積和內部結構,具有一定的質量等。但是,當我們...
等價模型equivalence models 是指系統在一定等價準則下的簡化模型。描寫系統行的模型有時是很複雜的,人們為了了解各主要因素間相互依賴關係,或是為了表達和計算,常在...
殼層模型是模擬原子內結構的結構模型。...... 這種將奇數原子核的性質視為僅由最後一個不成對的奇核子決定的簡化模型被稱為單粒子殼層模型,它在解釋原子核基態和...
一個實時系統模型由三個部分組成,調度與資源訪問控制、處理器和資源等,實時系統與通用作業系統不同,實時系統是套用在某個具體的場合中,且實時系統的任務必須在時限...
氣泡模型bubbling model是描述流化床反應器的一種簡化模型。它把流化床的全部流動特徵(如分布板結構、床層內部構件等)都歸結為以氣泡直徑來表示:與兩相模型相比較,...
《模型解題法》是慧之光教育“十一五”重點課題“優質教育資源評價與推廣”的子課題,也是該課題的最新研究成果。可以幫助孩子建立數理化思維,用最簡單的模組對應的...
採用Hoppe於1996年提出的遞進格線(PM)算法[1],可以生成多個連續的細節層次,方便地控制簡化的面數,同時簡化後頂點和對應的紋理不變,保證簡化模型的一致。...
通常,模型既要能基本反映現實情況,又須經過適當簡化,以便於套用。模型可分為物理模型和數學模型。物理模型是一個實物模型。建立物理模型的理論根據是“相似原理”。...
宏模型(Macromodel)是一種能夠模擬積體電路和系統靜態和動態特性的等效表示,它可以是電路、符號,也可以是數學公式或表格。宏模型建模方法主要有簡化法、構造法、列表...
矢量自回歸模型簡稱VAR模型,是一種常用的計量經濟模型,1980年由克里斯托弗·西姆斯(Christopher Sims)提出。VAR模型是用模型中所有當期變數對所有變數的若干滯後變數...
決策模型是用於經營決策的數學模型。由於社會經濟系統錯綜複雜,決策因素縱橫交錯,任何決策者僅憑直觀和經驗,都難以作出最優的決策。因此,在現代化的科學決策中,常常...
詞袋模型(英語:Bag-of-words model)是個在自然語言處理和信息檢索(IR)下被簡化的表達模型。...
單因素模型(Sharpe's One-way Analysis of Variance)是諾貝爾經濟學獎獲得者威廉·夏普(William Shape )在1963年發表《對於“資產組合”分析的簡化模型》一文中...
有些過程無法用理論分析方法導出其模型,但可通過試驗或直接由工業過程測定數據,經過數理統計法求得各變數之間的函式關係,稱為統計模型。...
在核物理與核化學中,核殼層模型是一個利用泡利不相容原理的結構來描述的原子核的能量級別的一個模型。原子核殼模型是邁耶(M.G.Mayer)夫人和簡森(J.H.D.Jensen...
物理問題的方便和探討物理事物的本身而對研究對象所作的一種簡化描述,是以觀察和實驗為基礎,採用理想化的辦法所創造的,能再現事物本質和內在特性的一種簡化模型。...
向量自回歸模型(簡稱VAR模型)是一種常用的計量經濟模型,由克里斯托弗·西姆斯(Christopher Sims)提出。它是AR模型的推廣。...
黑箱模型(Black box)或稱經驗模型,指一些其內部規律還很少為人們所知的現象。如生命科學、社會科學等方面的問題。但由於因素眾多、關係複雜,也可簡化為灰箱模型來...
分析模型是對客觀事物或現象的一種描述。模型是被研究對象的一種抽象。客觀事物或現象,是一個多因素綜合體。因素之間存在著相互依賴又相互制約的關係,通常是複雜的...
建模就是建立模型,就是為了理解事物而對事物做出的一種抽象,是對事物的一種無歧義的書面描述。建立系統模型的過程,又稱模型化。建模是研究系統的重要手段和前提。...
