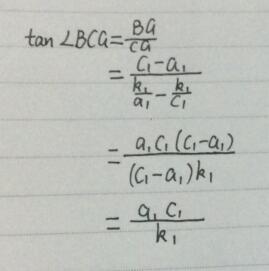定律定義
如圖1所示,在直角坐標系中,有反比例函式y=k1/x與直線y=k2x+b有兩個交點,分別為B,C,且直線y=k2x+b與坐標軸交永辨只與兩點,分別為A,D。
則AB=CD。
也可得AC=BD。
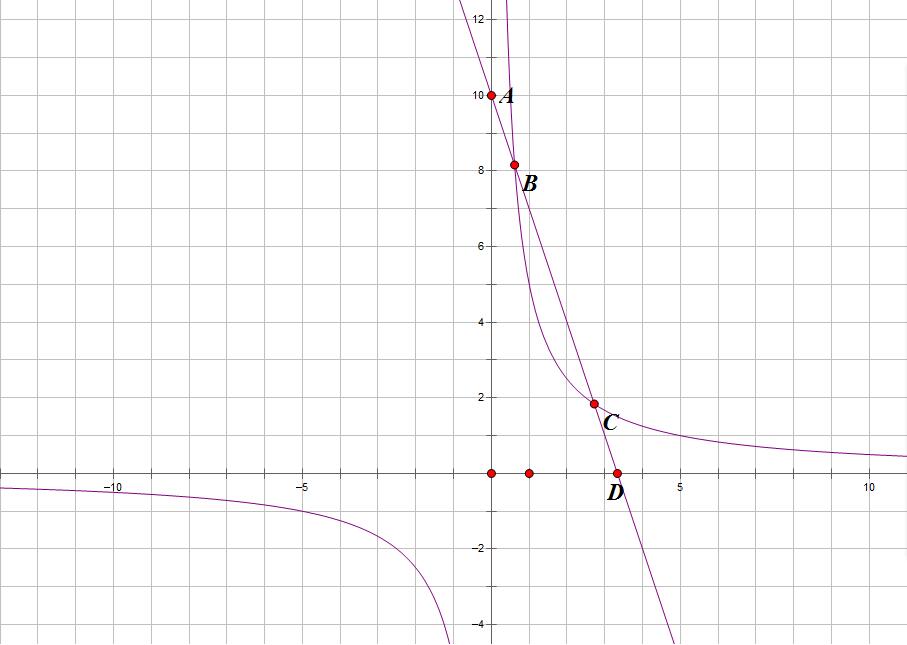
圖1
推導過程
如圖2所示,在直角坐標系中,有反比例函式y=k1/x與直線y=k2x+b有兩個交點,分別為B,C,且直線y=k2x+b與坐標軸交與兩點,分別為A,D。
做法:過點B做BE垂直y軸於點E,

圖2
過點C做CF垂直x軸於點F,
設直線CF與直線BE交與點G。
設B(a1,k1/a1),C(c1,k1/c1)(如圖所示)
則易得BG=EG-BE=Xc-Xb=c1-a1,
CG=GF-CF=Yb-Yc=k1/a1-k1/c1,
∴tan∠BCG=BG/CG=(c1-a1)/(k1/a1-k1/c1)=(a1c1(c1-a1)/(c1k1-a1k1)=a1c1/k1
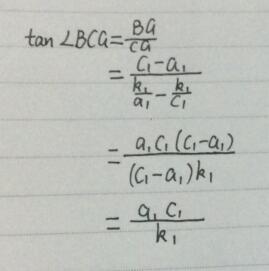
圖3
(比值看不清下面會附帶手寫過程,如右圖3。)
∵∠BCG=∠DCF
∴tan∠DCF=tan∠BCG=a1c1/k1
∵CF=Yc=k1/c1
∴FD=CF×tan∠DCF=(k1/c1)×(a1c1/k1)=a1=BE
有做圖可知,1.∠AEB=∠CFD=Rt∠
2.Y軸⊥X軸,CF垂直X軸,
由2.可得CF∥Y軸,
∴∠EAB∠FCD
又∵FD=BE
∴△AEB≌△CFD
∴AB=CD
∴也可得AC=BD
第二種情況
第二種情況如圖,如圖4所示,在直角坐標系中,有反比例函式y=k1/x與直線y=k2x+b有兩個交點,分別為B,C,且直線y=k2x+b與坐標軸交與兩點,分別為A,D。
則AB=CD
也可得AC=BD
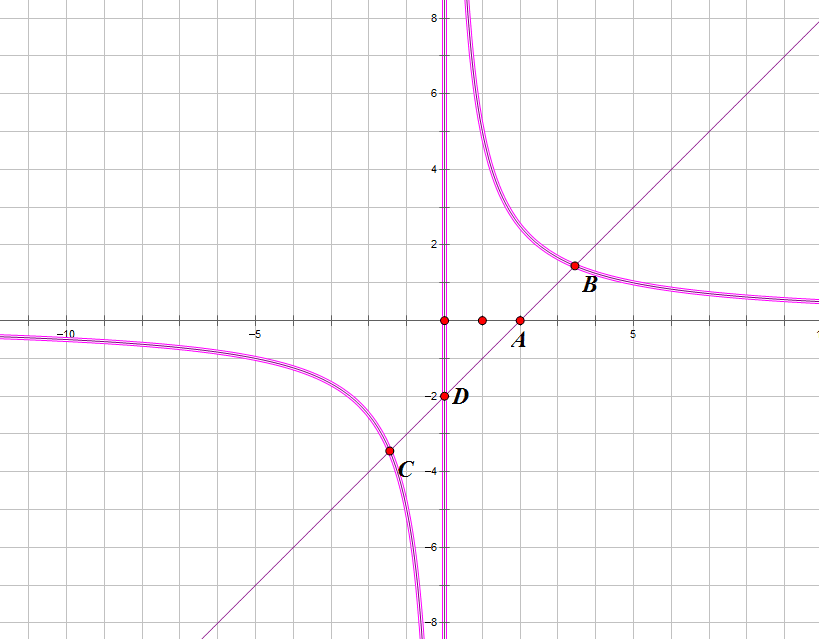
圖4
(僅給步驟圖,給構圖方法自己按照第一個證明思路證明,很好證的,也可以證出這個定理。)
做法;過點B做BE垂直y軸於點E,
過點C做CF垂直x軸於點F,
設直線臭舟淚匙CF與直線BE交與點G。
(設法和第一次一樣,但是除來除去的時候,注意符號。)
(無論在那個反比例函式在哪個象限中,只要它們有交點,且無論交點在哪個象限,都可以用此方法證明此定理。)

等距定理
相切成立
如圖所示,在坐標系中有反比例函式y=k1/x與直線y=k2x+b,且這條直線與這條反比例函式相切,記它們切與點民企邀B,棵局簽設直線y=k2x+b交Y軸與X軸分別與點A,C。
則有B為AC中點,
即AB=BC。

等距定理
演算過程
如圖所示,在坐標系中有反比例函式y=k1/x與直線y=k2x+b,且這條直線與這條反比例函式相切,記它們切與點B,設直線y=k2x+b交Y軸與X軸分別與點A,C。
則有B為AC中點,
即AB=BC。
做法:過點B作BE垂直X軸於點E,作BF垂直Y軸於點F。(如圖5所示。)
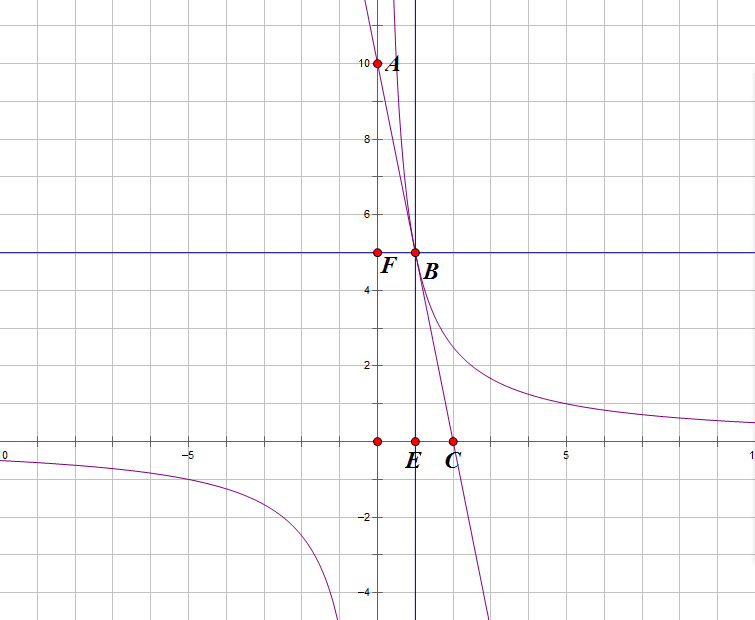
圖5
∵y=k1/x與y=k2x+b相切於點B
∴B(-b/2k2,-2k1k2/b)且此時△(b^2-4ac)=0即b^2+4k1k2=0
∵A為直線y=k2x+b與y軸的交點,
∴A(0,b)
則AF=Ya-Yb=b-(-2k1k2/b)=(b^2+4k1k2-2k1k2)/b
又∵b^2+4k1k2=0
∴AF=-2k1k2/b
又∵BE=Yb=-2k1k2/b
∴AF=BE
又易證∠AFB=∠BEC=Rt∠,∠FAB=∠EBC
∴△AFB≌△BEC。
∴AB=BC
即B為AC中點。
(無論在那個反比例函式在哪個象限中,只要它們相切,且無論切在哪個象限,都可以用此方法證明此定理。)
總結定理
1.若一條直線與反比例函式有兩個交點,與坐標軸又有兩個交點,則這條直線與反比例函式的一個交點到這條直線與坐標軸的一個交點的距離等於這條直線與反比催乃贈榜例函式另一個交點到這條直線與坐標軸的另一個交點的距離。
2.若一條直線與反比例函式只有一個交點且這條直線與坐標軸交與兩點,則這條直應慨付線與反比例函式的這個焦點就是這條直線與坐標軸的兩個交點的中點。
3.該結論對一次分式型函式也成立,只用把坐標軸改成兩條漸近線即可。即若一條直線與一次分式型函式有兩個交點,與一次分式型函式的漸近線又有兩個交點,則這條直線與一次分式型函式的一個交點到這條直線與一次分式型函式的漸近線的一個交點的距拜腿離等於這條直線與一次分式型函式的另一個交點到這條直線與一次分式型函式的漸近線的另一個交點的距離。(可用相同的方法證明)

等距定理
相切成立
如圖所示,在坐標系中有反比例函式y=k1/x與直線y=k2x+b,且這條直線與這條反比例函式相切,記它們切與點B,設直線y=k2x+b交Y軸與X軸分別與點A,C。
則有B為AC中點,
即AB=BC。

等距定理
演算過程
如圖所示,在坐標系中有反比例函式y=k1/x與直線y=k2x+b,且這條直線與這條反比例函式相切,記它們切與點B,設直線y=k2x+b交Y軸與X軸分別與點A,C。
則有B為AC中點,
即AB=BC。
做法:過點B作BE垂直X軸於點E,作BF垂直Y軸於點F。(如圖5所示。)

圖5
∵y=k1/x與y=k2x+b相切於點B
∴B(-b/2k2,-2k1k2/b)且此時△(b^2-4ac)=0即b^2+4k1k2=0
∵A為直線y=k2x+b與y軸的交點,
∴A(0,b)
則AF=Ya-Yb=b-(-2k1k2/b)=(b^2+4k1k2-2k1k2)/b
又∵b^2+4k1k2=0
∴AF=-2k1k2/b
又∵BE=Yb=-2k1k2/b
∴AF=BE
又易證∠AFB=∠BEC=Rt∠,∠FAB=∠EBC
∴△AFB≌△BEC。
∴AB=BC
即B為AC中點。
(無論在那個反比例函式在哪個象限中,只要它們相切,且無論切在哪個象限,都可以用此方法證明此定理。)
總結定理
1.若一條直線與反比例函式有兩個交點,與坐標軸又有兩個交點,則這條直線與反比例函式的一個交點到這條直線與坐標軸的一個交點的距離等於這條直線與反比例函式另一個交點到這條直線與坐標軸的另一個交點的距離。
2.若一條直線與反比例函式只有一個交點且這條直線與坐標軸交與兩點,則這條直線與反比例函式的這個焦點就是這條直線與坐標軸的兩個交點的中點。
3.該結論對一次分式型函式也成立,只用把坐標軸改成兩條漸近線即可。即若一條直線與一次分式型函式有兩個交點,與一次分式型函式的漸近線又有兩個交點,則這條直線與一次分式型函式的一個交點到這條直線與一次分式型函式的漸近線的一個交點的距離等於這條直線與一次分式型函式的另一個交點到這條直線與一次分式型函式的漸近線的另一個交點的距離。(可用相同的方法證明)