等腰梯形(英文:isosceles trapezium)按照數學領域可定義為:一組對邊平行(不相等),另一組對邊不平行但相等的四邊形。等腰梯形是一個平面圖形,是一種特殊的梯形。
基本介紹
- 中文名:等腰梯形
- 外文名:isosceles trapezoid
- 基本特徵:兩腰相等的梯形
- 面積公式:(上底+下底)×高÷2
- 周長公式:上底+下底+2×腰
- 歸屬學科:數學
定義

性質

 圖2 等腰梯形ABCD
圖2 等腰梯形ABCD


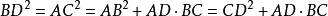
判定
面積公式

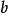



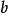

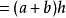
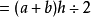
周長公式






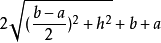
常用輔助線
 圖3常用輔助線
圖3常用輔助線
等腰梯形(英文:isosceles trapezium)按照數學領域可定義為:一組對邊平行(不相等),另一組對邊不平行但相等的四邊形。等腰梯形是一個平面圖形,是一種特殊的梯形。


 圖2 等腰梯形ABCD
圖2 等腰梯形ABCD


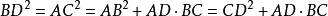





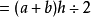

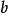





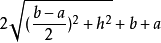
 圖3常用輔助線
圖3常用輔助線等腰梯形(英文:isosceles trapezium)按照數學領域可定義為:一組對邊平行(不相等),另一組對邊不平行但相等的四邊形。等腰梯形是一個平面圖形,是一種特殊的梯形。....
等腰梯形性質定理(英文:isosceles trapezium)是按數學領域可定義為:一組對邊平行(不相等),另一組對邊不平行但相等的四邊形的定理定律。...
梯形(trapezium)是指只有一組對邊平行的四邊形。平行的兩邊叫做梯形的底邊,較長的一條底邊叫下底,較短的一條底邊叫上底。另外兩邊叫腰;夾在兩底之間的垂線段...
等腰梯形判定定理是同一底邊上的兩個內角相等的梯形是等腰梯形。...... 同一底邊上的兩個內角相等的梯形是等腰梯形不相鄰的兩條邊相等的梯形是等腰梯形...
等邊梯形是指一組對邊平行而另一組對邊不平行的四邊形。...... 梯形是等腰梯形 3.同一底上的兩個角相等的梯形是等腰梯形 4.有一個內角是直角的梯形是直角梯...
梯形是指一組對邊平行而另一組對邊不平行的四邊形。平行的兩邊叫做梯形的底邊,其中長邊叫下底;不平行的兩邊叫腰;夾在兩底之間的垂線段叫梯形的高。一腰垂直...
等腰是一個漢語詞語,拼音是děng yāo,意思是具有兩條等邊的。...... ▪ 等腰三角形 ▪ 等腰梯形 等腰拼音 編輯 děng yāo ㄉㄥˇㄧㄠ等腰詞語解釋 編輯 ...
黃金梯形是指底角等於72゜的等腰梯形,其中AC=DC=BD,DC/AB的值為黃金比例。黃金梯形的比例勻稱,存在黃金分割率的黃金梯形能夠給畫面帶來美感,令人愉悅。...
上、下面平行且為長方形(特殊情況有兩個相對的面是正方形,即四稜台),四個側面都是梯形由此圍成的立體圖形叫梯形體...
等腰偏斜梯形是空間四邊形的一種。一個空間四邊形,如果存在一條直線同時垂直平分其一組對邊,則稱其為等腰偏斜梯形,而這條直線是它的對稱軸。從形狀上看,等腰...
梯形中位線定理是幾何學的一個定理,是指連線梯形兩腰中點的線段叫做梯形的中位線,梯形的中位線平行於兩底,並且等於兩底和的一半 。...
梯形螺紋是螺紋的一種,分為米制和英制兩種。 英制梯形螺紋的牙型角為29°,我國常見的是米制梯形螺紋,其牙型角為30°。牙型為等腰梯形,通常是用於一些機構的傳...
四稜台(Square frustum)一種特殊台梯形體(好比正方形與長方形),即底面與頂面均為正方形或長方形,側面都是等腰梯形,四條棱的延長線能夠交匯於一點的一種台體...
74等腰梯形性質定理 等腰梯形在同一底上的兩個角相等75等腰梯形的兩條對角線相等76等腰梯形判定定理 在同一底上的兩個角相等的梯形是等腰梯形...
