等腰梯形判定定理是同一底邊上的兩個內角相等的梯形是等腰梯形。
基本介紹
- 中文名:等腰梯形判定定理
- 性質:定理
- 學科:數學
- 特點:兩條對角線相等
判定
性質
例題
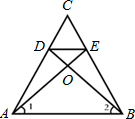
等腰梯形判定定理是同一底邊上的兩個內角相等的梯形是等腰梯形。

等腰梯形判定定理是同一底邊上的兩個內角相等的梯形是等腰梯形。...... 等腰梯形判定定理是同一底邊上的兩個內角相等的梯形是等腰梯形。中文名 等腰梯形判定定理 ...
等腰梯形性質定理(英文:isosceles trapezium)是按數學領域可定義為:一組對邊平行(不相等),另一組對邊不平行但相等的四邊形的定理定律。...
2、同一底上的兩個角相等的梯形是等腰梯形。3、對角線相等的梯形是等腰梯形。4、兩腰相等的梯形是等腰梯形以下判定不作為定理使用:...
∴四邊形ABCD為等腰梯形.提示:判定一個任意四邊形為等腰梯形,如果不能直接運用等腰梯形的判定定理,一般的方法是通過作輔助線,將此四邊形分解為熟悉的多邊形,此例就...
判定一個任意四邊形為等腰梯形,如果不能直接運用等腰梯形的判定定理,一般的方法是通過作輔助線,將此四邊形分解為熟悉的多邊形,此例就是通過作平行線,將四邊形分解...
∴四邊形ABCD為等腰梯形. 點評: 判定一個任意四邊形為等腰梯形,如果不能直接運用等腰梯形的判定定理,一般的方法是通過作輔助線,將此四邊形分解為熟悉的多邊形,此例...
平行四邊形判定定理矩形性質定理矩形判定定理菱形性質定理菱形判定定理菱形面積公式正方形性質定理正方形判定定理等腰梯形判定定理等腰梯形性質定理...
74等腰梯形性質定理 等腰梯形在同一底上的兩個角相等75等腰梯形的兩條對角線相等76等腰梯形判定定理 在同一底上的兩個角相等的梯形是等腰梯形...
74等腰梯形性質定理 等腰梯形在同一底上的兩個角相等75等腰梯形的兩條對角線相等76等腰梯形判定定理 在同一底上的兩個角相等的梯形是等腰梯形...
74等腰梯形性質定理等腰梯形在同一底上的兩個角相等75等腰梯形的兩條對角線相等76等腰梯形判定定理在同一底上的兩個角相等的梯形是等腰梯形...
74、等腰梯形性質定理:等腰梯形在同一底上的兩個角相等75、等腰梯形的兩條對角線相等76、等腰梯形判定定理:在同一底上的兩個角相等的梯形是等腰梯形...
在應試教育中,只有多記公式定理,掌握解題技巧,熟悉各種題型,才能在考試中取得最好的成績。在高考中只會做題是不行的,一定要在會的基礎上加個“熟練”才行,小題...
125 船矩形性質定理的推論 126 矩形的判定定理 127 菱形的性質 128 菱形的面積公式 129 菱形的判定定理 130 正方形的判定 131 等腰梯形的性質與判定 ...
74等腰梯形性質定理 等腰梯形在同一底上的兩個角相等 75等腰梯形的兩條對角線相等 76等腰梯形判定定理在同一底上的兩個角相等的梯形是等腰梯形 77對角線相等的梯...
選擇題 判斷題 證明題 未知數 大於號 小於號恆等號 不等號 公分母 不等式 ...凸多邊形 平行線段逆否命題 對稱中心 等腰梯形 等分線段比例線段 勾股定理 黃金...
32.3 矩形、菱形的性質定理和判定定理及其證明32.4 等腰梯形的性質定理和判定定理及其證明本章檢測第三十三章 機率的計算和估計33.1 用列舉法求機率...
將國中數理化公式、定理、定律和實驗編撰成簡明手冊,是國中生學習和考試的必備...4.3梯形[梯形][直角梯形][等腰梯形][等腰梯形性質定理][等腰梯形判定定理][...
等腰梯形的判定 梯形的中位線 梯形中位線定理 梯形的面積 第五章 相似形 兩條線段的比 比的前項與後項 成比例線段 組成比例的項 比例外項 比例內項 第四比...
74等腰梯形性質定理 等腰梯形在同一底上的兩個角相等75等腰梯形的兩條對角線相等76等腰梯形判定定理 在同一底上的兩個角相等的梯形是等腰梯形77對角線相等的梯形...
