基本介紹
- 中文名:平行公設
- 外文名:parallel postulate
- 別名:平行公理、第五公設
- 提出者:歐幾里得
- 適用領域:數學
- 套用學科:幾何學
第五公設一般指本詞條
平行公設(parallel postulate),也稱為平行公理、歐幾里得第五公設,因是《幾何原本》五條公設的第五條而得名。這是歐幾里得幾何一條與眾不同的公理,比前四條複雜。公設是說:如果一條線段與兩條直線相交,在某一側的內角和小於兩直角和,那么這兩條直線在不斷延伸後,會在內角和小於兩直角和的一側相交。簡介 ...
這兩個幾何系統的相異之處僅在於一個承認第五公設而不承認羅氏公設,另一個則承認羅氏公設而不承認第五公設.除此而外的其餘公設、公理、定義及基本概念均相同. 人們把這兩個幾何系統中的相同的部分(即一切相同的公設、公理、定義及基本概念)所構成的幾何系統稱為絕對幾何.故歐氏幾何由絕對幾何外加第五公設構成,...
第五公設(即平行公設)內容複雜,陳述累贅,缺乏象其它公設和公理那樣的說服力,並不自明。因此,它能否正確地反映空間形式的性質,引起了古代學者們的懷疑。從古希臘時代到公元18世紀,人們通過不同的途徑和方法對這一問題進行了大量的研究工作,其中薩克里( Saccheri,1667—1733)和蘭勃特( Lambert,1728-1777)等人...
第三公設 第三公設的內容是:以任意點為心以及任意距離(即半徑)可畫圓 第三公設的內容是:以任意點為心以及任意距離(即半徑)可畫圓.這是歐幾里德在其著作《幾何原本》中提出來的.在《幾何原本》中,他一共提出了五條公設,這五條公設被用來證明所有的其他歐氏幾何的命題.在五條公設中,以第五公設最為著名.
皮亞諾的這五條公理用非形式化的方法敘述如下:1是自然數;每一個確定的自然數a,都有一個確定的後繼數a',a'也是自然數(一個數的後繼數就是緊接在這個數後面的數,例如,1的後繼數是2,2的後繼數是3等等);對於每個自然數b、c,b=c若且唯若b的後繼數=c的後繼數;1不是任何自然數的後繼數;...
第五公理又叫做平行公理 (the parallel axiom),因為它等價於:過直線外一點,可作且只可作一直線跟此直線平行。五條一般公理 (a,b,c,d 皆為正數)1.跟同一個量相等的兩個量相等;即若 a=c 且 b=c,則 a = b(等量代換公理)。2.等量加等量,其和相等;即若 a=b 且 c=d,則 a+c = b+d...
皮亞諾的這五條公理用非形式化的方法敘述如下:Ⅰ、0是自然數;Ⅱ、每一個確定的自然數a,都具有確定的後繼數a' ,a'也是自然數(數a的後繼數a'就是緊接在這個數後面的整數(a+1)。例如:1'=2,2'=3等等。);可是僅有這兩個公理還不夠完整地描述自然數,因為滿足這兩條的有可能不是自然數系統。
平行公理 在歐幾里得的幾何原本中,第五公設(又稱為平行公理)是關於平行線的性質。它的陳述是:“如果兩條直線被第三條直線所截,一側的同旁內角之和大於兩個直角,那么最初的兩條直線相交於這對同旁內角的另一側。”這條公理的陳述過於冗長。在1795年,蘇格蘭數學家Playfair提出了以下公理作為平行公理的代替,在...
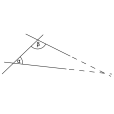
第五公設是論及平行線的,它說的是:如果一直線和兩直線相交,且所構成的兩個同側內角之和小於兩直角,那么,把這兩直線延長,它們一定在那兩內角的一側相交。數學家們並不懷疑這個命題的真實性,而是認為它無論在語句的長度,還是在內容上都不大像是個公設,而倒像是個可以證明的定理,只是由於歐幾里得沒能找到...
其中公理五又稱之為平行公設(Parallel Postulate),敘述比較複雜,並不像其他公理那么顯然。這個公設衍生出“三角形內角和等於一百八十度”的定理。在高斯(F. Gauss)的時代,公設五就備受質疑,俄羅斯數學家羅巴切夫斯基(Nikolay Ivanovitch Lobachevski)、匈牙利人波爾約(Bolyai)闡明第五公設只是公理系統的一種可能...
其內角和為 1800,當然還要不以第五公設為基礎.然而種種努力依然未能成功.經過仔細分析,在這種失敗的“證明” 中,依然是憑藉於圖形的直觀而默認了一個假定: “至少存在一個銳角,從它的某一邊上的任意點作垂線,必與另一邊有交點.”實際上,這一被默認的假定仍然是第五公設的一個等價命題,其後被稱為“銳角...
第五公設(同平面內一條直線和另外兩條直線相交,若某側的同旁內角之和小於180°,則這兩條直線在這一側一定相交)可以說是歐幾里得幾何公理系統里最富爭議的一條公設了。由於它在《幾何原本》中只用到過一次,很多數學家都在懷疑它是一個公設還是一條定理。為此,有無數人曾試圖用另外九條基本命題來證明第五...
其中公設五又稱之為平行公設(Parallel Axiom),敘述比較複雜,這個公設衍生出“三角形內角和等於一百八十度”的定理。在高斯(F. Gauss,1777年—1855年)的時代,公設五就備受質疑,俄羅斯數學家羅巴切夫斯基(Nikolay Ivanovitch Lobachevski)、匈牙利人波約(Bolyai)闡明第五公設只是公理系統的一種可能選擇,並非必然...
當然還有最受爭議的第五公設(平行公設)。這些問題困擾著數學家多年,他們希望可將《幾何原本》的定義、公設和公理加以改善,但因為幾何學有堅實的基礎,且有不少互相關聯的分支,如:雙曲幾何、球面幾何、射影幾何等等,更使數學家不可只關心個別的公理或定義,而必須提供一整套關於概念和公理、定理的嚴密的系統,...
應該指出,非歐幾何為廣大數學界接受還是經過幾番艱苦鬥爭的。首先要證明第五公設的否定並不會導致矛盾,只有這樣才能說新幾何學成立,才能說明第五公設獨立於別的公理公設,這是一個起碼的要求。當時證明的方法是證明“相對無矛盾性”。因為當時大家都承認歐幾里得幾何學沒有矛盾,如果能把非歐幾何學用歐幾里得幾何學...
《下金蛋的數學問題》是2020年人民郵電出版社出版的圖書,作者是韓雪濤。內容簡介 本書介紹了從代數、幾何、圖論、數論中採擷出的6 個經典數學問題。第一章介紹多項式方程根式解問題。第二章介紹幾何三大問題,即用尺規三等分角、倍立方,以及化圓為方。第三章介紹歐幾里得第五公設問題。第四章介紹四色問題。第五章...
在歐氏幾何與解析幾何的發展過程中,人們不斷發現《幾何原本》在邏輯上不夠嚴密,並不斷地充實一些公理,特別是在嘗試用其他公理、公設證明第五公設“一條直線與另外兩條直線相交,同側的內角和小於兩直角時,這兩條直線就在這一側相交”的失敗,促使人們重新考察幾何學的邏輯基礎,並取得了兩方面的突出研究成果。一...
但數學常不被稱為經驗科學,甚至有時稱為形上學,因為數學往往是從幾個公理出發演繹出的理論體系。如《幾何原本》僅由五個公理就演繹出厚厚一本書來,而把其中第五公設變了變,又演繹出《羅氏幾何》和《黎曼幾何》。數學的公理往往來源於直覺,所以又常常被稱為先驗科學,其實它與經驗科學沒有太大的本質區別,...
第五章 幾何學與拓撲學的發展 41.“以算代證”證明命題——解析幾何的誕生 42.可以變形的圖形——仿射幾何 43.用微積分來解決幾何問題——微分幾何的誕生 44.用代數研究幾何——代數幾何的歷史 45.第五公設的難題——非歐幾何的誕生 46.幾何學的統領——廣義黎曼幾何 47.海岸線有多長——分形幾何學 48.七...
你把它渲染上一層浪漫色彩,結果就弄得像是在歐幾里得第五公設里摻進了戀愛故事一樣了。”還有在《格蘭其莊園》中他說道:“我承認你很會選材,這彌補了你敘述不夠得力的缺陷。但你看待一切問題總是從寫故事的角度出發,而不是從科學破案的角度,這樣就毀壞了這些典型案例的示範性。你把偵破的技巧和細節一筆帶...
皮亞諾的這五條公理用非形式化的方法敘述如下:Ⅰ 0是自然數;Ⅱ 每一個確定的自然數a,都有一個確定的後繼數a' ,a' 也是自然數(數a的後繼數a' 就是緊接在這個數後面的數(a+1),例如,1’=2,2‘=3等等);Ⅲ 如果b、c都是自然數a的後繼數,那么b = c;Ⅳ 0不是任何自然數的後繼數;...
第6 章 兩朵烏雲……… 069 第7 章 物理學的奇蹟年……… 081 第8 章 雙生子佯謬……… 099 第9 章 第五公設……… 116 第10 章 彎曲的時空……… 131 第11 章 宇宙常數……… 145 第12 章 開天眼……… 157 第13 章 核火球………...
上下求索兩千年一一第五公設問題 公主巧施圍地計——等周問題 “神機”與“妙算”——數學計算工具演進問題 中國古代數學中的奇葩——割圓術問題 自然界的奇特建築——蜂房問題 數學中的維納斯——對數問題 騎士城堡中的數學一一哥尼斯堡七橋問題 腓特烈大帝閱兵式——歐拉方陣問題 第四篇 催人淚下的科學蒙難大...
