穩態誤差是系統從一個穩態過渡到新的穩態,或系統受擾動作用又重新平衡後,系統出現的偏差。穩態誤差記作ess(Steady-State Errors)。
基本介紹
- 中文名:穩態誤差
- 外文名:穩態誤差
- 解釋:自動控制系統在穩態控制精度度量
- 分類:原理性誤差和實際性誤差兩類
名詞解釋
 穩態誤差
穩態誤差穩態誤差的分類
 穩態誤差
穩態誤差原理性誤差

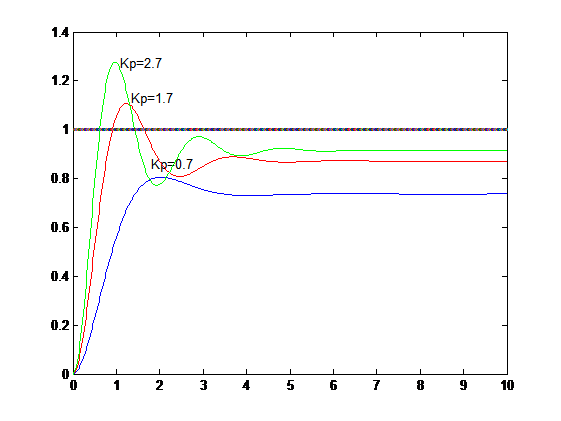
穩態誤差是系統從一個穩態過渡到新的穩態,或系統受擾動作用又重新平衡後,系統出現的偏差。穩態誤差記作ess(Steady-State Errors)。
 穩態誤差
穩態誤差 穩態誤差
穩態誤差
穩態誤差是系統從一個穩態過渡到新的穩態,或系統受擾動作用又重新平衡後,系統出現的偏差。穩態誤差記作ess(Steady-State Errors)。...
穩態誤差係數(Steady State Error Coefficient),即靜態誤差係數,是為了方便反映控制系統穩態誤差而設定的係數。對不同的輸入量加以區分,主要有靜態位置誤差係數、靜態...
要求自動控制系統中,在一段時間內控制系統被控制量的偏差(穩態誤差)為零或在允許的範圍之內的性能指標。...
動態誤差係數(dynamic error coefficient)是控制系統穩態精度的一種度量。...... 靜態誤差係數只適於刻畫穩態誤差是常數的系統,動態誤差係數可用來描述系統穩態誤差隨時...
動態誤差dynamic error,是指在被測量隨時間變化過程中進行測量時所產生的附加誤差稱為動態誤差。...
跟蹤誤差是指在定位運動或者電機運動過程中,從開始運動到實際位置的時間段內的位置命令與實際位置的差值,跟蹤誤差在各個行業裡面有的一定的誤差認可範圍。...
靜態誤差係數分為靜態位置誤差係數、靜態速度誤差係數、靜態加速度誤差係數。分別代表了控制系統中,一個系統對階躍輸入、斜坡輸入、拋物線信號輸入回響消除或減少穩態...
PID控制的基礎是比例控制;積分控制可消除穩態誤差,但可能增加超調;微分控制可加快大慣性系統回響速度以及減弱超調趨勢。 這個理論和套用的關鍵是,做出正確的測量和...
控制性能就是控制系統的性能,其評價分為動態性能指標和穩態性能指標兩類。系統的動態過程提供系統穩定性、回響速度及阻尼情況,表現為衰減、發散、等幅振盪等形式,由...
穩是指系統的穩定性(stability),一個系統要能正常工作,首先必須是穩定的,從階躍回響上看應該是收斂的;準是指控制系統的準確性、控 制精度,通常用穩態誤差來(...
余差是指工業PID控制系統中,比例調節器的輸入、輸出量之間存在著對應的比例關係,變化量經比例調節達到平衡時,不能加復到給定值時的偏差。一般的,余差即穩態誤差...
比例控制存在穩態誤差,增大K可減小穩態誤差,但不能消除。對於干擾較大、慣性較大的系統,不宜採用比例控制。積分閥是靠積分控制的,他是在比例的控制上加上積分控制...
有靜差系統(systems with steady state error) 是指控制系統按穩態誤差分類時的一種形式.對於某類輸入,穩態誤差不為零的系統。...
無靜差系統(systems without steady state er- ror)控制系統按穩態誤差分類時的一種形式.是對於某類輸入的穩態誤差為零的系統。...
動態誤差 dynamic error 控制系統在任意的輸入信號作用下達到穩態時的控制誤差。通常,動態誤差的概念都假定是線上性定常系統(見線性系統、定常系統)的情形下加以...
