基本介紹
- 中文名:移位暫存器序列
- 外文名:shift register sequence
- 所屬學科:數學(組合設計)
- 簡介:反饋移位暫存器產生的偽隨機碼
- 簡稱:移存器序列
基本介紹



相關說明
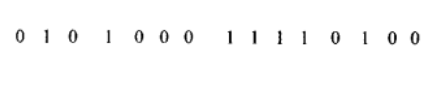
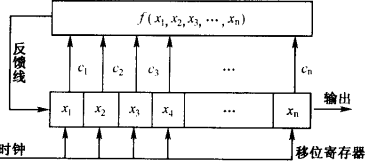

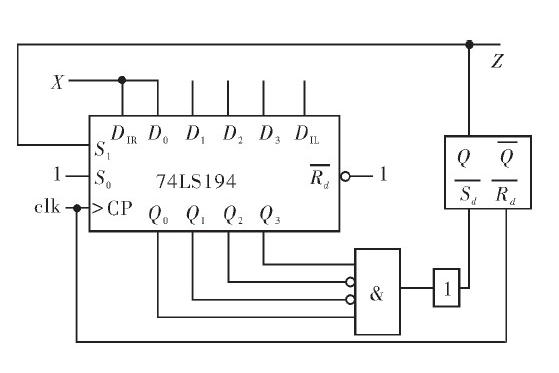







移位暫存器序列(shift register sequence)是一類重要的碼,它是數字通信中利用反饋移位暫存器產生的一種偽隨機碼,由初始狀態(x₁,x₂,…,xn)依反饋邏輯函式xn+1=f(x₁,x₂,…,xn)產生...
m序列是CDMA系統中採用的最基本的PN序列。 是最長線性反饋移位暫存器序列的簡稱。簡介 m序列是最長線性反饋移位暫存器序列的簡稱。它是由帶線性反饋的移存器產生的周期最長的序列。一般來說,一個n級線性反饋移存器可能產生的最長周期等於(2^n -1)。m序列是一種典型的偽隨機序列。在通信領域有著廣泛的套用,如...
移位暫存器是產生信號和序列的常用設備,它分為線性和非線性兩大類,著名的一序列和序列就是分別由線性和非線性反饋移位暫存器所生成的。線性反饋移位暫存器(Linear feedback shift register,LFSR)是 通常由動態或靜態主從型觸發器構成。反饋迴路由異或門構成。其特性通常由一個特徵多項式表征。使用二輸入異或門計算...
c、用移位暫存器和反饋組合電路(分立門電路,解碼器,多路復用器)設計 分類 根據結構不同,它可分為反饋移位型和計數型兩種:移位型序列信號發生器信號發生器 信號發生器又稱信號源或振盪器,它是指產生所需參數的電測試信號的儀器。在生產實踐和科技領域中有著廣泛的套用。按信號波形可分為正弦信號、函式(波形...
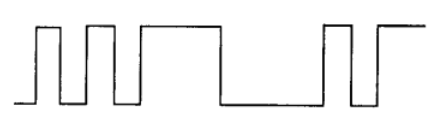
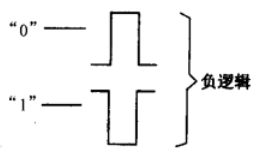
周期達到2n-1的序列稱為最長線性移位暫存器序列,簡稱M序列,圖中b就是三級M序列,它的輸出為…,0,0,1,0,1,1,1,…。M序列完全滿足偽隨機序列的三點要求,特別是它的相關函式為因而是典型的偽隨機序列。M序列的周期一定是2n-1,實用上還需要有其他的周期,這可用非線性移位暫存器序列得到。n級非線性移位...
偽噪聲序列(PN序列,Pseudo-noise Sequence)是指具有類似隨機噪聲的一些統計特性,但和真正的隨機信號不同,它可以重複產生和處理,故稱作偽隨機噪聲序列。PN序列有多種,其中最基本最常用的一種是最長線性反饋移位暫存器序列,也稱作m序列,通常由反饋移位暫存器產生。其最重要的特性是對所有時間延遲自相關值低,或者...
次冪個長為N=2ⁿ的完全循環。事實上,每個長為N=2ⁿ的德布萊英序列恰與德布萊英圖Gₙ中的一條完全迴路相對應。De Bruijn序列的套用與性質簡介 De Bruijn序列是一類重要的非線性移位暫存器序列,它在通信及密碼等領域內有著極為廣泛的套用,複雜度是刻劃這類序列特性的一個重要概念。具有良好偽隨機性質的二元...
《無線通信中的序列設計原理》是2007年國防工業出版社出版的圖書,作者是曾凡鑫。內容簡介 《無線通信中的序列設計原理》以直接序列擴譜通信、跳頻擴譜通信和超寬頻跳時衝激無線電為套用平台,系統闡述了適合於直接序列擴譜通信系統的基於反饋移位暫存器序列理論的擴譜序列設計方法;闡述了適合於跳頻通信系統的具有至多一次...
之所以稱其為偽隨機序列,是因為它表現出白噪聲採樣序列的統計特性,在不知其生成方法的偵聽者看來像真的隨機序列一樣。M序列作為一種基本的PN序列,具有很強的系統性、規律性和相關性。M序列的理論發展比較成熟。實現比較簡便,利用n級移位暫存器可產生長度為2“一l的M序列。目前,3G移動通信技術仍是通信領域的...
對於非線性反饋移位暫存器的研究,利用代數學的知識,刻畫了一些具有對稱反饋函式的非線性反饋移位暫存器生成序列的最小周期;通過分析一類具有可約特徵多項式的線性反饋移位暫存器的圈結構和鄰接圖,給出了由這些線性反饋移位暫存器產生最大長度非線性反饋移位暫存器的算法,得到了一批de Bruijn序列;利用符號計算和Grobner基...
利用卷積碼進行快速相關攻擊時,首先將相關攻擊問題轉化為低碼率卷積碼的解碼,然後用最大似然解碼算法恢復出移位暫存器的初態。快速相關攻擊的攻擊效果主要與相關性的大小、移位暫存器序列生成多項式的非零項數和已知序列段的長度有關。是分析序列密碼算法的基本工具之一。發布者:中國軍事百科全書編審室 ...
我們把這種具有最大長度周期的線性移位暫存器序列稱為最大長度線性移位暫存器序列,又稱為m序列。前面介紹的四級線性移位暫存器序列就是一個m序列。m序列是同樣級數的線性移位暫存器所產生的最大長度序列,因此它的效率是最高的,這是m序列的一個優點。m序列的最主要優點是,它具有某種隨機性,尤其是它的自相關函式...
,即序列周期為 的移位暫存器序列是最大長度序列,否則就是非最大長度序列。常見偽隨機信號 1、m序列 m序列是最大長度線性移位暫存器序列。2、M序列 由非線性反饋邏輯和移位暫存器構成的序列發生器所能產生的最大長度序列,叫做最大長度非線性移位暫存器序列,簡稱M序列。若移位暫存器的級數為n,則M序列的最大長度...
《密碼學講義》是2010年科學出版社出版的圖書,作者是李超、屈龍江。內容簡介 《密碼學講義》從數學的角度較為系統地介紹了序列密碼、分組密碼和公鑰密碼的基本理論與方法,利用周期序列的冪級數表示、根表示和跡表示研究了線性反饋移位暫存器序列及其變種的密碼學性質;利用圖論和組合數學等工具研究了非線性反饋移位暫存器...
m序列具有類似於隨機信號較好的自相關特性。m序列由線性反饋移位暫存器加權產生。根據反饋係數的取值不同,電路可以產生出各種具有不同特性的數字序列。對於一定的移位暫存器級數r,存在一些特殊的Ci取值,使得輸出序列的周期達到最長,即為2?1。這樣的序列被稱為最長線性反饋移位暫存器序列,即m序列。光同步數字傳輸系統...
該方法先檢測收到碼信號中的PN碼,通過開關,送入n級PN碼發生器的移位暫存器。待整個碼序列全部進入填滿後,在相關器中,將產生的PN碼與收到的碼信號進行相關運算,在比較器中將所得結果與門限進行比較。若未超過門限,則繼續上述過程。若超過門限,則停止搜尋,系統轉入跟蹤狀態。理想情況下,捕獲時Ts=nTc,(Tc...
完成擾碼和解擾的電路相應地稱為擾碼器和解擾器,擾碼器實際上就是偽隨機序列發生器。偽隨機序列是由數字電路產生的周期序列,但具有類似隨機噪聲的一些統計特性,因此稱為偽隨機序列或偽噪聲序列。其中m序列(最長線性反饋移位暫存器序列)具有很好的偽噪聲性質,並且產生方法比較簡單,所以最為常用。關於偽隨機序列的基本...
全書共分9章,第1章介紹密碼學中的一些基本概念,第2章介紹古典密碼的加密方法和一些典型的古典密碼體制,第3章介紹Shannon的密碼學理論,第4章和第5章分別討論分組密碼和公鑰密碼,第6章介紹序列密碼和線性移位暫存器序列,第7章和第8章分別討論數字簽名和Hash函式,第9章介紹一些重要的密碼協定。《高等院校信息...
《信息安全數學基礎》是2006年8月清華大學出版社出版的圖書,作者是覃中平。內容簡介 本書介紹了群、環、域、數論、組合論、移位暫存器序列、計算複雜性、資訊理論與數理邏輯等諸多與信息安全相關聯的數學基礎內容。本書以大量的例題說明數學的抽象概念對信息安全中的諸多對象的本質刻畫。本書內容全面系統,包括信息安全...
6.2 移位暫存器與移位暫存器序列 6.3 線性反饋移位暫存器的表示 6.3.l 線性反饋移位暫存器的一元多項式表示 6.3.2 線性移位暫存器序列的周期性 6.3.3 線性移位暫存器的序列空間 6.4 線性移位暫存器序列的極小多項式 6.5 m序列的偽隨機性 6.6 流密碼的破譯 6.6.1 流密碼中的主要攻擊方法 6.6.2 m序列...
它是由兩個10級反饋移位暫存器構成的C碼產生的。兩個移位暫存器於每星期日子夜零時,在置“1”脈衝作用下全處於1狀態,同時在碼率1.023MHZ驅動下,兩個移位暫存器分別產生碼長為N=2''1= 1023,周期為Ims的兩個m序列G(t)和G2(t)。C2(t)序列經過相位選擇器,輸人一個與G2()平移等價的m序列,然後與G(t...
然而,通過本原多項式,線性反饋移位暫存器可以生成看起來是隨機的且循環周期非常長的序列。線性反饋移位暫存器的套用包括生成偽隨機數,偽隨機噪聲序列,快速數字計數器,還有擾頻器。線性反饋移位暫存器在硬體和軟體方面的套用都非常得普遍。循環冗餘校驗中用於快速校驗傳輸錯誤的數學原理,就與線性反饋移位暫存器密切相關。
最簡單的擾碼方法是在輸入數字序列上加一個最長線性移位暫存器序列,使前者變換為信道序列;相應地在接收端從信道序列中減去同步的同一最長移位暫存器序列,可還原為原數字序列。這個方法在電路上不難實現。這種方法的另一優點是:當信道序列在傳輸中出現碼元差錯時,不會因為加有解擾器而使差錯傳播。這個方法存在的問題...
《有限域上若干問題的研究》是依託中國科學院數學與系統科學研究院,由周凱擔任項目負責人的青年科學基金項目。項目摘要 無論是有限域上的各種正規基,具有各種特性的置換多項式,流密碼學以為基礎理論的線性移位暫存器序列,還是有限域上的典型群等等,這些對象之間都有著天然的內在緊密聯繫,對它們的交叉研究既有著數學...
作者用兩章篇幅,以儘量少的抽象數學概念和語言來闡述這些編碼理論所需要的代數知識,然後介紹編碼理論中的兩類碼,即第三章的偽隨機序列和第四章的糾錯碼。第三章完整地介紹了移位暫存器序列,特別是線性移位暫存器序列的理論。第四章介紹了幾類重要的糾錯碼。最後在第五章,介紹了編碼理論中出現的幾個代數問題。
第二部分講述數論、代數和組合學在通信中的一些主要套用,包括廣義布爾函式和它的有限傅立葉變換、移位暫存器序列、糾錯碼和信息安全。《代數與通信》可作為高等學校數學系信息專業本科生和計算機與通信系本科生或研究生的專業基礎課或選修課教材或參考書。圖書目錄 第一部分 數論與代數 第1章 初等數論 1.1 整除性和...
第6章介紹流密碼和線性移位暫存器序列。第7章和第8章分別討論數字簽名和Hash函式。第9章介紹了一些重要的密碼協定。每章後面均附有習題,其中部分習題是對正文內容的補充。本書除校正了第一版中的一些排印錯誤外,在內容上也做了一些修改和增補,特別是對第四章中的分組密碼的結構和工作模式進行了補充,並在第五...
