非線性反饋移位暫存器（NLFSR, Nonlinear feedback shift register）是相對於線性反饋移位暫存器而言的。
基本介紹
- 中文名：非線性反饋移位暫存器
- 外文名：Nonlinear feedback shift register
- 縮寫：NLFSR
- 相關術語：線性反饋移位暫存器
簡介,線性反饋移位暫存器,Fibonacci LFSRs,Galois LFSRs,參見,
簡介
非線性反饋移位暫存器（NLFSR, Nonlinear feedback shift register）是相對於線性反饋移位暫存器而言的。它們的大體電路邏輯相似，僅僅在於NLFSR的反饋邏輯是由異或門和與門構成的，而LFSR中僅存在異或門。從代數表達式來看，異或門是加法（+），而與門是乘法（*）。由加法構成的反饋邏輯，其反饋表達式的最高項次數不會增長，而由乘法參與的反饋表達式項次數會增長、並可能超過定義多項式的最高項。
線性反饋移位暫存器
線性反饋移位暫存器（英語：Linear feedback shift register，LFSR）是指給定前一狀態的輸出，將該輸出的線性函式再用作輸入的移位暫存器。異或運算是最常見的單比特線性函式：對暫存器的某些位進行異或操作後作為輸入，再對暫存器中的各比特進行整體移位。
賦給暫存器的初始值叫做“種子”，因為線性反饋移位暫存器的運算是確定性的，所以，由暫存器所生成的數據流完全決定於暫存器當時或者之前的狀態。而且，由於暫存器的狀態是有限的，它最終肯定會是一個重複的循環。然而，通過本原多項式，線性反饋移位暫存器可以生成看起來是隨機的且循環周期非常長的序列。
循環冗餘校驗中用於快速校驗傳輸錯誤的數學原理，就與線性反饋移位暫存器密切相關。
Fibonacci LFSRs
圖中白色數字為抽頭，與表中本原多項式相對應，則暫存器的循環周期為最大，65535（不包括全零狀態）。圖中的狀態為 0xACE1 (十六進制) 下一個狀態是 0x5670。
影響下一個狀態的比特位叫做抽頭。圖中，抽頭序列為[16,14,13,11]。
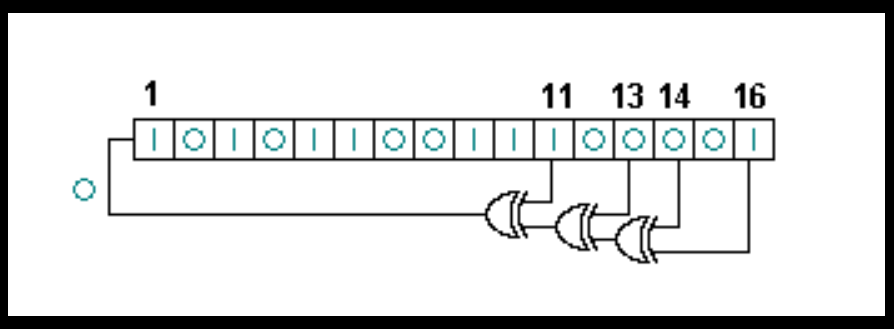一個 16-位 Fibonacci LFSRLFSR最右端的比特為輸出比特。抽頭依次與輸出比特進行異或運算，然後反饋回最左端的位。最右端位置所生成的序列被稱為輸出流。
- 影響LFSR下一個狀態的比特位叫做抽頭（圖中白色數字）
- 最大長度的LFSR生成一個M序列（例如，只有與有一定抽序列的LFSR才能通過所有 2−1 個內部狀態，不包括全零狀態），除非它本身為全零，亦即狀態永不改變
- 作為基於異或運算的LFSR的替換，LFSR也可以給予同或運算。與使用異或門的LFSR全零狀態下為無效狀態相應的，使用同或門的LFSR在全“1”狀態下也是無效的。
有LFSR或者基於同或門的LFSR生成的序列可以被認為是同格雷碼或者自然二進制碼同樣有效的二進制序列。
在LFSR中，抽頭的設定可以用有限域算數中模2的多項式來表示。這就意味著，多項式中的所有係數必須是“1”或者“0”。這個多項式被稱作回授多項式或特徵多項式。例如圖中的抽頭為在第16，14，13，11個比特，則相應的特徵多項式為：
多項式中常數“1”並不代表某一個抽頭，它所指的是一個比特位的輸入（例如x,等效為 1 ）。多項式中的指數代表從左至右的抽頭位。第一個和最後一個比特一般相應的是輸入和輸出位。
若且唯若相應的回授多項式是本原多項式時，LFSR才能達到最大長度。這表示以下條件是必須的：
- 抽頭的數量必須為偶數。
- 抽頭之間不能成對出現，必須是互質的。
生成最長LFSRs的本原多項式表可通過下部的連結找到。 這類型LFSR也被成為標準，多對一或外部異或門的LFSR。下一節將會介紹Galois型的LFSR。
Galois LFSRs
以法國數學家埃瓦里斯特·伽羅瓦命名，是LFSRs的Galois型結構。
