典型的二進制格雷碼(Binary Gray Code)簡稱格雷碼,因1953年公開的弗蘭克·格雷(Frank Gray,18870913-19690523)專利“Pulse Code Communication”而得名,當初是為了通信,現在則常用於模擬-數字轉換和位置-數字轉換中。法國電訊工程師波特(Jean-Maurice-Émile Baudot,18450911-19030328)在1880年曾用過的波特碼相當於它的一種變形。1941年George Stibitz設計的一種8元二進制機械計數器正好符合格雷碼計數器的計數規律。
格雷碼(Gray code)曾用過Grey Code、葛萊碼、葛蘭碼、格萊碼、戈萊碼、循環碼、二進制反射碼、最小差錯碼等名字,它們有的是錯誤的,有的易與其它名稱混淆,建議不再使用它們。
基本介紹
- 中文名:格雷碼
- 外文名:Binary Gray Code
- 全稱:二進制格雷碼
- 提出者:弗蘭克·格雷
- 提出時間:1940年
概述
碼錶
| 十進制數 | 4位自然二進制碼 | 4位典型格雷碼 | 十進制餘三格雷碼 | 十進制空六格雷碼 | 十進制跳六格雷碼 | 步進碼 |
|---|---|---|---|---|---|---|
0 | 0000 | 0000 | 0010 | 0000 | 0000 | 00000 |
1 | 0001 | 0001 | 0110 | 0001 | 0001 | 00001 |
2 | 0010 | 0011 | 0111 | 0011 | 0011 | 00011 |
3 | 0011 | 0010 | 0101 | 0010 | 0010 | 00111 |
4 | 0100 | 0110 | 0100 | 0110 | 0110 | 01111 |
5 | 0101 | 0111 | 1100 | 1110 | 0111 | 11111 |
6 | 0110 | 0101 | 1101 | 1010 | 0101 | 11110 |
7 | 0111 | 0100 | 1111 | 1011 | 0100 | 11100 |
8 | 1000 | 1100 | 1110 | 1001 | 1100 | 11000 |
9 | 1001 | 1101 | 1010 | 1000 | 1000 | 10000 |
10 | 1010 | 1111 | ---- | ---- | ---- | ---- |
11 | 1011 | 1110 | ---- | ---- | ---- | ---- |
12 | 1100 | 1010 | ---- | ---- | ---- | ---- |
13 | 1101 | 1011 | ---- | ---- | ---- | ---- |
14 | 1110 | 1001 | ---- | ---- | ---- | ---- |
15 | 1111 | 1000 | ---- | ---- | ---- | ---- |
特點
- 格雷碼是一種絕對編碼方式,典型格雷碼是一種具有反射特性和循環特性的單步自補碼,它的循環、單步特性消除了隨機取數時出現重大誤差的可能,它的反射、自補特性使得求反非常方便。
- 由於格雷碼是一種變權碼,每一位碼沒有固定的大小,很難直接進行比較大小和算術運算,也不能直接轉換成液位信號,要經過一次碼變換,變成自然二進制碼,再由上位機讀取。
- 典型格雷碼是一種採用絕對編碼方式的準權碼,其權的絕對值為2^i-1(設最低位i=1)。
- 格雷碼的十進制數奇偶性與其碼字中1的個數的奇偶性相同。
發展歷史
轉換方法
遞歸生成碼錶
- 1位格雷碼有兩個碼字
- (n+1)位格雷碼中的前2n個碼字等於n位格雷碼的碼字,按順序書寫,加前綴0
- (n+1)位格雷碼中的後2n個碼字等於n位格雷碼的碼字,按逆序書寫,加前綴1
- n+1位格雷碼的集合 = n位格雷碼集合(順序)加前綴0 + n位格雷碼集合(逆序)加前綴1
| 2位格雷碼 | 3位格雷碼 | 4位格雷碼 | 4位自然二進制碼 |
|---|---|---|---|
00 | 000 | 0000 | 0000 |
01 | 001 | 0001 | 0001 |
11 | 011 | 0011 | 0010 |
10 | 010 | 0010 | 0011 |
110 | 0110 | 0100 | |
111 | 0111 | 0101 | |
101 | 0101 | 0110 | |
100 | 0100 | 0111 | |
1100 | 1000 | ||
1101 | 1001 | ||
1111 | 1010 | ||
1110 | 1011 | ||
1010 | 1100 | ||
1011 | 1101 | ||
1001 | 1110 | ||
1000 | 1111 | ||
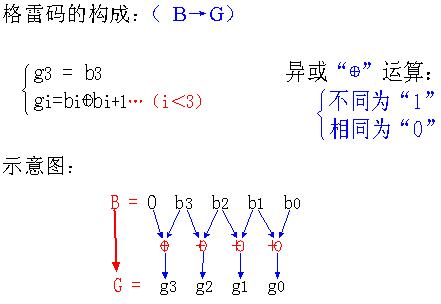
異或轉換
- 對n位二進制的碼字,從右到左,以0到n-1編號
- 如果二進制碼字的第i位和i+1位相同,則對應的格雷碼的第i位為0,否則為1(當i+1=n時,二進制碼字的第n位被認為是0,即第n-1位不變)


利用卡諾圖
- 將卡諾圖變數分為兩組,變數數目相近(最好相等)
- 以邏輯變數高位在左低位在右建立卡諾圖
- 從卡諾圖的左上角以之字形到右上角最後到左下角遍歷卡諾圖,依次經過格子的變數取值即為典型格雷碼的順序
AB╲ C | 0 | 1 |
00 | 0→ | 1↓ |
01 | ↓2 | ←3 |
11 | 6→ | 7↓ |
10 | 4 | ←5 |
AB╲CD | 00 | 01 | 11 | 10 |
00 | 0→ | 1→ | 3→ | 2↓ |
01 | ↓4 | ←5 | ←7 | ←6 |
11 | 12→ | 13→ | 15→ | 14↓ |
10 | 8 | ←9 | ←11 | ←10 |
使用異或乘除
套用
角度感測器
 編碼盤
編碼盤格雷碼
九連環問題
程式實現
#include<stdio.h>voidmain(){ intm,n,i,j,b,p,bound; intgr[14];//輸入n,m並判斷m是否合法 bound=1; printf("Pleaseinputtwonumber:n,m\n"); scanf("%d,%d",&n,&m); for(i=1;i<=n;i++) bound*=2; if(m<0||m>=bound) { printf("Dataerror!"); exit(0); } b=1; for(i=0;i<n;i++) { p=0; b*=2; for(j=0;j<=m;j++) { if(j%b-b/2==0) p=1-p; } gr[i]=p; } printf("m="); for(i=n-1;i>=0;i--) { printf("%d",gr[i]); } printf("\n");}var x,y,i:longint;begin readln(x); fori:=30downto0do begin y:=(xand(1shli))xor((xand(1shl(i+1)))shr1); x:=xandnot(1shli)ory; end; writeln(x);end.2var x,i,n:longint;begin readln(n); x:=n; fori:=1to31do begin x:=xshr1; n:=nxorx; end; writeln(n);end.

