在各種計算機語言中，如C、C++、java等，使用按位異或的思想執行的操作。異或邏輯的關係是：當AB不同時，輸出P=1；當AB相同時，輸出P=0。“⊕”是異或數學運算符號，異或邏輯也是與或非邏輯的組合，其邏輯表達式為：P=A⊕B。在計算機語言中，異或的符號為” ^ “。
基本介紹
- 中文名：異或操作
- 外文名：the operation of XOR
- 邏輯：當AB不同時輸出1，相同時輸出0
- 符號：^
- 邏輯表達式：P=A⊕B
- 數學運算符號：⊕
簡介,運算法則,作用,交換參數值,奇偶判斷,格雷碼,奇數分頻,
簡介
異或操作就是在各種計算機語言中，如C、C++、java等，使用按位異或的思想執行的操作。異或操作滿足結合律和交換律，則由其性質可知，在計算機語言中，實現一些功能，例如參數的交換，奇偶性的判斷等，使用異或操作就會變得非常簡單。除此之外，還可以使用計算機語言進行其他更多的套用，接下來會對其作用做一些介紹。
運算法則
1）交換律：a ^ b = b ^ a。
2）結合律：a ^ b ^ c = a ^ （b ^ c） = （a ^ b） ^ c；
d = a ^ b ^ c 可以推出 a = d ^ b ^ c。
3）自反性：a ^ b ^ a = b。
異或運算最常見於多項式除法，不過它最重要的性質還是自反性：
A^B^ B=A，即對給定的數A，用同樣的運算因子（B）作兩次異或運算後仍得到A本身。這是一個神奇的性質，利用這個性質，可以獲得許多有趣的套用。例如，所有的程式教科書都會向初學者指出，要交換兩個變數的值，必須要引入一個中間變數。但如果使用異或，就可以節約一個變數的存儲空間：
設有A，B兩個變數，存儲的值分別為a，b，則以下三行表達式將互換他們的值表達式（值）：
A=A^B（a^b）；
B=B^A（b^a^b=a）；
A=A^B（a^b^a=b）。
類似地，該運算還可以套用在加密，數據傳輸，校驗等等許多領域。
x是二進制數0101；
y是二進制數1011；
則結果為x^y=1110；
0^0=0；0^1=1；1^0=1；1^1=0；
只有在兩個比較的位不同時其結果是1，否則結果為0。
即“相同為0，不同為1”。
輸入 | 運算符 | 輸入 | 結果 |
1 | ^ | 0 | 1 |
1 | ^ | 1 | 0 |
0 | ^ | 0 | 0 |
0 | ^ | 1 | 1 |
作用
在各種計算機語言中，異或操作通常用在位運算中。主要有如下幾個作用：
交換參數值
例：a = 8；b = 12
a=a^b； 1000^1100=0100
b=b^a； 1100^0100=1000
a=a^b； 0100^1000=1100
則a = 12；b = 8
奇偶判斷
^a操作就是將a中的每一位按位逐一進行異或，例如a=1010，則b=1^0^1^0=0，由此可以判斷a中為1的位數是奇數還是偶數。
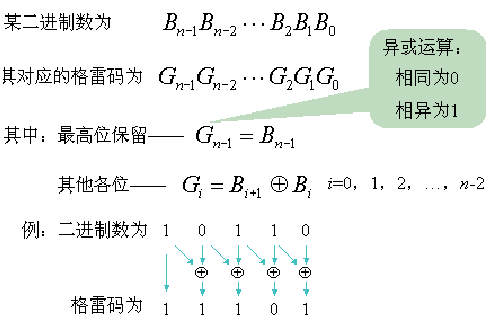
格雷碼
格雷碼（Graycode）是由貝爾實驗室的FrankGray在1940年提出，用於在PCM（PusleCodeModulation）方法傳送訊號時防止出錯，並於1953年三月十七日取得美國專利。格雷碼是一個數列集合，相鄰兩數間只有一個位元改變，為無權數碼，且格雷碼的順序不是唯一的。
以二進制為0值的格雷碼為第零項，第一項改變最右邊的位元，第二項改變右起第一個為1的位元的左邊位元，第三、四項方法同第一、二項，如此反覆，即可排列出n個位元的格雷碼。
1、自然二進制碼轉換成二進制格雷碼
自然二進制碼轉換成二進制格雷碼，其法則是保留自然二進制碼的最高位作為格雷碼的最高位，而次高位格雷碼為二進制碼的高位與次高位相異或，而格雷碼其餘各位與次高位的求法相類似。
自然二進制碼轉換成二進制格雷碼，其法則是保留自然二進制碼的最高位作為格雷碼的最高位，而次高位格雷碼為二進制碼的高位與次高位相異或，而格雷碼其餘各位與次高位的求法相類似。
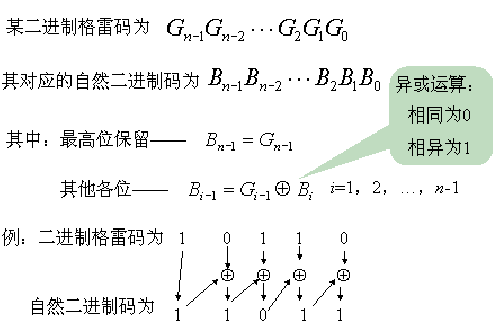
2、二進制格雷碼轉換成自然二進制碼
二進制格雷碼轉換成自然二進制碼，其法則是保留格雷碼的最高位作為自然二進制碼的最高位，而次高位自然二進制碼為高位自然二進制碼與次高位格雷碼相異或，而自然二進制碼的其餘各位與次高位自然二進制碼的求法相類似。
二進制格雷碼轉換成自然二進制碼，其法則是保留格雷碼的最高位作為自然二進制碼的最高位，而次高位自然二進制碼為高位自然二進制碼與次高位格雷碼相異或，而自然二進制碼的其餘各位與次高位自然二進制碼的求法相類似。
奇數分頻
1、奇數分頻電路：
奇數分頻電路常用的是錯位“異或”法的原理。如進行三分頻，通過待分頻時鐘的上升沿觸發計數器進行模三技術，當計數器計數到鄰近值進行兩次翻轉。比如計數器在計數到1時，輸出時鐘進行翻轉，計數到2時再進行翻轉，即在鄰近的1和2時刻進行兩次翻轉。這樣實現的三分頻占空比為1/3或2/3.如果要實現占空比為50%的三分頻時鐘，可通過待分頻的時鐘上升沿觸發計數器和下降沿觸發計數器進行三分頻，然後將上升沿和下降沿產生的三分頻時鐘進行相或預算，即可得到占空比為50%的三分頻時鐘。
2、錯位“異或”法推廣：
對於實現占空比為50%的N倍奇數分頻，首先進行上升沿觸發的模N計數，計數到某一選定值時，進行輸出時鐘翻轉，然後進過（N-1）/2再次進行翻轉得到一個占空比非50%的技術分頻時鐘。再者同時進行下降沿觸發的模N計數，到和上升沿觸發輸出時鐘翻轉選定值相同時，進行輸出時鐘翻轉，同樣經過（n-1）/2時，輸出時鐘再次翻轉生成占空比非50%的奇數N分頻時鐘。兩個占空比非50%的時鐘相或運算，得到占空比為50%的奇數N分頻時鐘。
