瞬心為互相作平面相對運動的兩構件上,瞬時相對速度為零的點。也可以說就是瞬時速度相等的重合點(即等速重合點)。若該點的絕對速度為零則為絕對瞬心,若不等於零則為相對瞬心。
基本介紹
簡介
特點
瞬心求法
 直接觀察法
直接觀察法 三心定理
三心定理瞬心數目
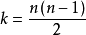
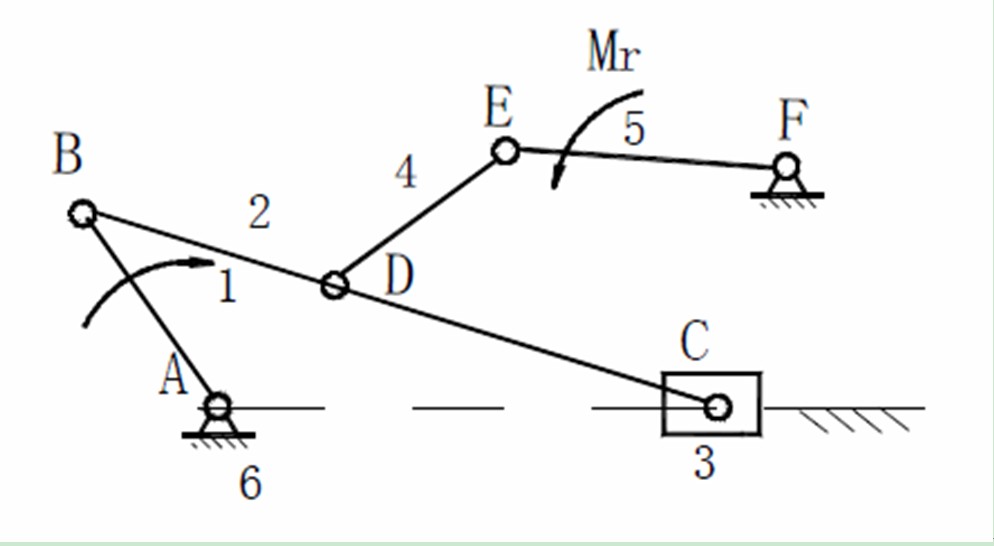
瞬心為互相作平面相對運動的兩構件上,瞬時相對速度為零的點。也可以說就是瞬時速度相等的重合點(即等速重合點)。若該點的絕對速度為零則為絕對瞬心,若不等於零則為相對瞬心。
 直接觀察法
直接觀察法 三心定理
三心定理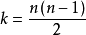
瞬心為互相作平面相對運動的兩構件上,瞬時相對速度為零的點。也可以說就是瞬時速度相等的重合點(即等速重合點)。若該點的絕對速度為零則為絕對瞬心,若不等於零...
在某一瞬間,平面圖形內速度等於0的點稱為速度瞬心。...... 由理論力學可知,互作平面相對運動的兩構件上(在研究的時候,有時瞬心不在圖紙所繪機構或構件上,這時可...
瞬心為互相作平面相對運動的兩構件上,瞬時相對速度為零的點。也可以說就是瞬時速度相等的重合點(即等速重合點)。若該點的絕對速度為零則為絕對瞬心,若不等於零...
平面運動剛體任一瞬時,絕對加速度為零的點稱為加速度瞬心。一般情況下,剛體可看做在瞬時,繞加速度瞬心做定軸轉動。各點絕對加速度方向不再與點到瞬心連線垂直,...
速度瞬心(簡稱瞬心):若該點是互作平面相對運動兩構件上瞬時相對速度為零、或者說絕對速度相等的重合點,故瞬心可定義為兩構件上的瞬時等速重合點。...
瞬心文化發展股份有限公司於2017年05月03日成立。法定代表人王小東,公司經營範圍包括:服務:製作、複製、發行:專題、專欄、綜藝、卡通片、廣播劇、電視劇、電影,經營...
瞬心為互相作平面相對運動的兩構件上,瞬時相對速度為零的點。也可以說就是瞬時速度相等的重合點(即等速重合點)。若該點的絕對速度為零則為絕對瞬心,若不等於零...
這說明瞬心里還是在牽掛著遙,牽掛著或許心裡也在暗暗後悔的事。 然後小剛像專家一樣的說:“小遙那裡已經有沙織小姐了,剩下的就是男生同志了。”...
三心定理,當兩構件直接組成運動副時,其瞬心的位置可以很容易地通過直接觀察加以確定;如果兩構件沒有直接連線形成運動副,則它們的瞬心位置需要用三心定理來確定。三...
共軛曲線是指兩構件上用以實現給定運動規律的連續相切的一對曲線,作為平面運動的一對共軛曲線與一對瞬心線(見瞬心)相同之處都是點接觸,但瞬心線之間是純滾動,而...
Poid 英文單詞Poid [pɔid] n.形心(曲線); 擬正弦線; 膺正弦線; 瞬心軌跡Poid 品牌About Poid (關於 Poid) Poid源自英國,是一個電子時尚的傳播者。Poid...
確定瞬心後,平面圖形上任一點D的速度矢量可表示為。 平面圖形在定平面上運動時,瞬心的位置不斷變化,瞬心在平面圖形上的軌跡稱為動瞬心軌跡;瞬心在定平面上的軌跡...
如果在固定平面L上建立固定的坐標系O-XY,在薄片的A點上建立運動的坐標系A-xy,則速度瞬心C在固定平面上(即相對於O-XY)的軌跡為空間極跡,而速度瞬心C在薄片上...
