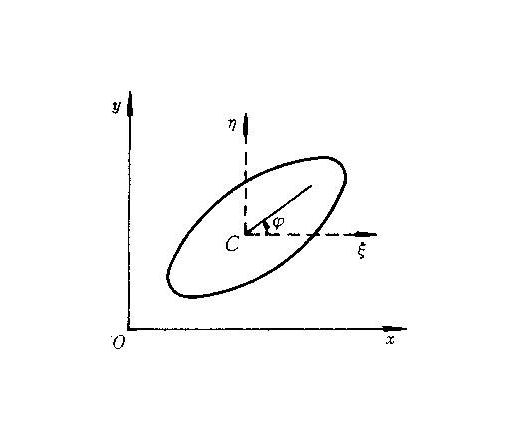
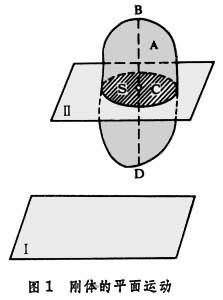
在運動中剛體上任一點和某一固定平面的距離保持不變。如圖1中的剛體A作平行於固定平面I的平行運動。在這種運動中,剛體上每一條垂直於固定平面的直線(如匘)上的各點都作相同的運動,如果作一個和平面Ⅰ平行的固定平面Ⅱ, 並且它在剛體A上截出一平面圖形S,則剛體的平面運動即歸結為平面圖形S在固定平面Ⅱ中的運動。在工程技術中,剛體的平面運動是常見的一種運動形式,如沿直線軌道滾動的車輪;曲柄連桿機構中的連桿等。
剛體平面運動的速度和加速度 平面圖形S(圖2)在定平面Ⅱ中的運動可以分解成隨基點的平動和繞基點的轉動。因此,平面圖形上任一點D的速度矢量為
式中為基點的速度矢量;為由於的變化而引起的平面圖形的角速度矢量。角速度同基點的選擇無關。平面圖形上任一點D的加速度矢量為
式中為基點的加速度矢量;為平面圖形的角加速度矢量。
瞬時轉動中心 根據歐拉轉動定律,平面圖形在固定平面中的任一有限位移總可以用對某一中心作一次轉動達到。因而平面圖形在任一瞬時的運動可看成為繞某一中心以某一角速度作瞬時轉動,此中心稱為平面圖形的瞬時轉動中心。因該點的瞬時速度為零,故又稱為瞬時速度中心或簡稱瞬心。例如,沿著直線軌道作無滑動的滾動車輪,它同地面的接觸點即為瞬心。套用瞬心求圖形上任一點的速度的方法稱為瞬心法,為此需要確定瞬心的位置。當已知基點的速度矢量和剛體的角速度矢量時,瞬心C┡可由公式確定。通常用幾何法來確定瞬心的位置。在剛體上任取兩點E、E┡,過此兩點分別作速度矢量、的垂線,有以下幾種情況(圖3)。
剛體的平面運動① 兩垂線相交則交點C┡即為瞬心(圖3a);②兩垂線重合則連線矢量和的末端作直線和公垂線相交,交點┡即為瞬心(圖3b和3c);③如兩垂線既不相交也不重合(圖3d),或在②中的兩直線平行(圖3e),則平面圖形作瞬時平動,瞬心在無窮遠處。確定瞬心後,平面圖形上任一點D的速度矢量可表示為。
平面圖形在定平面上運動時,瞬心的位置不斷變化,瞬心在平面圖形上的軌跡稱為動瞬心軌跡;瞬心在定平面上的軌跡稱為定瞬心軌跡。平面圖形的運動可看成動瞬心軌跡在定瞬心軌跡上作無滑動的滾動。例如,車輪在直線軌道上作無滑動的滾動時,車輪的外圓周為動瞬心軌跡,軌道為定瞬心軌跡。
動力學方程 剛體平面運動的動力學方程為=,=,或寫成微分形式,式中為質心的加速度;為剛體對於過質心並垂直於固定平面的軸的轉動慣量;為作用在剛體上的外力系對此軸的合力矩;為角加速度矢量<在該軸上的投影;為剛體的質量;為作用在剛體上的外力系的主矢量。
剛體作平面運動時,其動能,式中為質心的速度的大小。剛體的動量為,對過質心且垂直於固定平面的軸的角動量為。
 剛體的平面運動
剛體的平面運動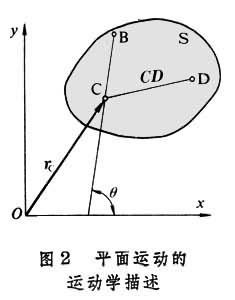 剛體的平面運動
剛體的平面運動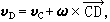 剛體的平面運動
剛體的平面運動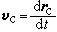 剛體的平面運動
剛體的平面運動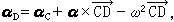 剛體的平面運動
剛體的平面運動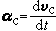 剛體的平面運動
剛體的平面運動 剛體的平面運動
剛體的平面運動 剛體的平面運動
剛體的平面運動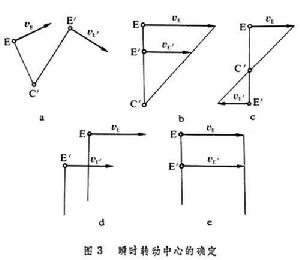 剛體的平面運動
剛體的平面運動 剛體的平面運動
剛體的平面運動 剛體的平面運動
剛體的平面運動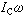 剛體的平面運動
剛體的平面運動