概念
在剛體平面運動中,只要剛體上任一平行於某固定平面的截面圖形S(或其延伸)在任何瞬時的角速度
w不為零,就必有速度為零的一點P',稱為速度瞬心。在該瞬時,就速度分布而言,截面圖形(或其延伸)好象只是在繞固定平面上重合於P'的一點P而轉動,點P稱為轉動瞬心。例如車輪在地面上作無滑動的滾動時,車輪接觸地面的點P'就是速度瞬心,而地面上同P'相接觸的點P就是轉動瞬心。
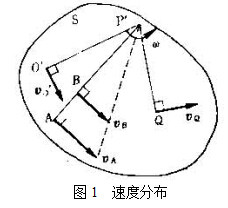
如取點P'作基點,則圖形S上各點的速度如圖1所示,其中
因此,如已知圖形的速度瞬心和該瞬時的角速度
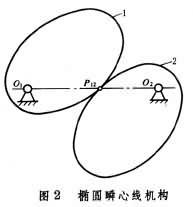
w,即可求出平面運動剛體上各點的瞬時速度。圖形S運動時,速度瞬心不斷地遷移,在圖形上留下一條隨圖形一起運動的幾何軌跡圖A'P'B'(圖2),稱為動瞬心軌跡;與此同時,轉動瞬心P也在不斷地改變位置,在固定平面上留下一條幾何軌跡APB,稱為定瞬心軌跡。這兩條軌跡在該瞬時的瞬心處相切,且對應的弧段具有相等的長度。因此,圖形S在運動時便攜帶著動瞬心軌跡A'P'B'在定瞬心軌跡APB上作無滑動的滾動(純滾動)。由此得到潘索定理:平面圖形的運動可用它的動瞬心軌跡在定瞬心軌跡上的純滾動來代替。例如,圖3上橢圓規尺的AB兩端分別沿軸Ox和Oy滑動,規尺AB的動瞬心軌跡是圓心為O'的小圓,定瞬心軌跡是圓心為O的大圓。規尺AB的平而運動可由小圓O'在固定大圓O上的純滾動來代替。
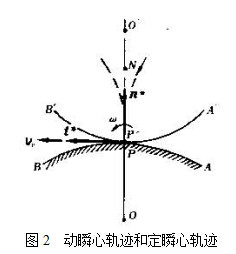
圖2上畫出了兩條瞬心軌跡在切點處的切向和法向單位矢t*和n*。兩瞬心軌跡的曲率中心分別為O'和O。兩軌跡的曲率半徑分別為
於是,可求得約化曲率半徑
上式中,當O'和O在公切線兩側時取正號,反之取負號。瞬心沿其軌跡遷移時,具有遷移速度
速度瞬心必在圖形S各點速度矢量的垂線上,且各點的速度大小與其距離成正比,由此很容易確定瞬心的位置。例如,對於圖4上所示的曲柄連桿機構,已知連桿上A、B兩點的速度
Va和
Vb的方向互不平行,連桿的速度瞬心C必是過A,B所作
Va、Vb的兩垂線的交點。當曲柄OA轉到鉛直位置時,出現特殊情況,這時
Va和
Vb平行,它們的垂線AC和BC也平行,因而速度瞬心C落到無窮遠處。這種運動狀態稱為瞬時平動,在這瞬時,連桿上各點的速度都相同,而角速度
Wab則等於零(見剛體的平動)。
位置
由理論力學可知,互作平面
相對運動的兩
構件上(在研究的時候,有時
瞬心不在圖紙所繪機構或構件上,這時可以認為相關構件是延伸或無限延伸的,研究所用構件只是現實中的構件的最簡化結構形式)瞬時速度相等的重合點,即為此兩構件的速度瞬心(instantaneous centre of velocity)。
在理論力學中
瞬心也被作為瞬時速度中心,即做平面運動的剛體 剛體或者剛體延伸部分上的唯一一個瞬時速度為零的點
瞬心數目
因為發生
相對運動的任意兩
構件之間具有一個
瞬心,所以根據排列組合的原理,如果一個機構是由k個構件組合而成,那么它的瞬心的總數為:
N=〔k(k-1)〕∕2
套用
在剛體平面運動中,只要剛體上任一平行於某固定平面的截面圖形S(或其延伸)在任何瞬時的角速度ω不為零,就必有速度為零的一點P′,稱為速度
瞬心。在該瞬時,就
速度分布而言,截面圖形(或其延伸)好像只是在繞固定平面上重合於P′的一點P而轉動,點P稱為轉動
瞬心。例如車輪在地面上作無滑動的滾動時,車輪接觸地面的點P′就是速度
瞬心,而地面上同P′相接觸的點P就是轉動
瞬心。
如取點P′作基點,則圖形S上各點的速度如圖1所示,其中vQ=ω×,因此,如已知圖形的速度
瞬心和該瞬時的角速度ω,即可求出
平面運動剛體上各點的瞬時速度。圖形S運動時,速度
瞬心不斷地遷移,在圖形上留下一條隨圖形一起運動的
幾何軌跡A′P′B′,稱為動
瞬心軌跡;與此同時,轉動
瞬心P也在不斷地改變位置,在固定平面上留下一條幾何軌跡APB,稱為定瞬心軌跡。這兩條軌跡在該瞬時的
瞬心處相切,且對應的弧段具有相等的長度。因此,圖形S在運動時便攜帶著動
瞬心軌跡A′P′B′在定瞬心軌跡APB上作無滑動的滾動(
純滾動)。由此得到潘索定理:
平面圖形的運動可用它的動
瞬心軌跡在定瞬心軌跡上的
純滾動來代替。例如,圖3上橢圓規尺AB的兩端分別沿軸Ox和Oy滑動,規尺AB的動瞬心軌跡是
圓心為O′的小圓,定瞬心軌跡是圓心為O的大圓。規尺AB的平面運動可由小圓O′在固定大圓O上的
純滾動來代替。
兩條瞬心軌跡在
切點處的切向和
法向單位矢t*和n*。 兩瞬心軌跡的
曲率中心分別為O′和O。兩軌跡的曲率半徑分別為ρ′=P′O′,ρ=PO;於是,可求得約化曲率半徑。
上式中,當O′和O在
公切線兩側時取正號,反之取負號。
瞬心沿其軌跡遷移時,具有遷移速度。
速度
瞬心必在圖形S各
點速度矢量的垂線上,且各點的速度大小與其距離成正比,由此很容易確定瞬心的位置。例如,對於圖4上所示的曲柄連桿機構,已知連桿上A、B兩點的速度vA和vB的方向互不平行,連桿的速度
瞬心C必是過A,B所作vA、vB的兩垂線的交點。當曲柄OA轉到鉛直位置時,出現特殊情況,這時vA和vB平行,它們的垂線AC和BC也平行,因而速度
瞬心C落到無窮遠處。 這種
運動狀態稱為瞬時
平動,在這瞬時,連桿上各點的速度都相同,而
角速度則等於零(見剛體的平動)。