基本介紹
- 中文名:直接解析開拓
- 外文名:direct analytic continuation
- 所屬學科:數學
- 所屬問題:複變函數論(黎曼曲面)
- 相關概念:解析開拓原理、解析函式等
基本介紹



















其他解釋及概念
解析開拓











解析元素


解析開拓原理






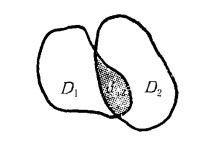














































直接解析開拓(direct analytic continuation)是滿足解析開拓原理的兩解析元素。若給定兩個解析元素{D1,f(z)}及{D2,f(z)},D1和D2互不包含,其公共部分是一...
對於擴充後的函式元素,同樣可以定義直接開拓,及沿平面弧的解析開拓。極元素及代數函式的直接開拓是正則元素。對於擴大的函式元素類,給定一個函式元素,沿平面上所有弧...
D1時,F(z)=f1(z);當 z∈Γ時,F(z)=f1(z)=f2(z);當z∈D2時,F(z)=f2(z),此時稱{D1,f1(z)}及{D2,f2(z)}互為越過弧Γ的直接解析開拓。
解析開拓鏈是相繼為直接解析開拓的解析元素集合。若每一個解析元素都是前一個解析元素的直接解析開拓,則稱這些解析元素組成解析開拓鏈,並稱{D1,f1(z)}及{Dn,...
基於魏爾斯特拉斯的定義,區域上的解析函式可以看作是其內任一小圓鄰域上冪級數的解析開拓 ,關於解析開拓的一般定義是,f(z)與g(z)分別是D與D*上的解析函式,...
是完全解析函式的一個元素,圓心在點 z 處,它可由元素 用圓心在點 的有限元素鏈得出,其中每後一個元素都是前一元素的直接解析開拓。不是一般性,可以設諸點 有...
若每一個解析元素都是前一個解析元素的直接解析開拓,則稱這些解析元素組成解析開拓鏈,並稱{D1,f1(z)}及{Dn,fn(z)}互為解析開拓。
班勒衛定理是對關於越過弧線的直接解析開拓。直接解析開拓是滿足解析開拓原理的兩解析元素。中文名 班勒衛定理 外文名 Painleve theorem 適用範圍 數理科學 目錄 1 ...
1.在區域DUsUD’內解析;2.在D內有F(z)=f(z);3.在D’內有F(z)=f*(z*);則稱{D’ , F(z)}是{D,f(z)}的越過S的直接解析開拓....
則稱 是{D,f(z)}的越過S的直接解析開拓。黎曼-施瓦茲對稱原理解析元素 編輯 解析元素亦稱解析函式元素,或簡稱函式元素,是單值解析函式及其定義域組成的二元組。
