無窮時滯泛函微分方程(functional differentialequation with infinite delay)一類具有無界滯量的特殊的滯後型泛函微分方程.具有無界滯量或滯量在無窮區間上分布的方程稱為無窮時滯泛函微分方程.
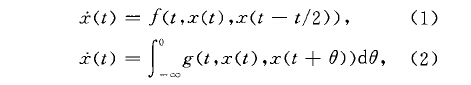

無窮時滯泛函微分方程(functional differentialequation with infinite delay)一類具有無界滯量的特殊的滯後型泛函微分方程.具有無界滯量或滯量在無窮區間上分布的方程稱為無窮時滯泛函微分方程.
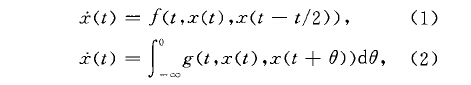

泛函微分方程(functional differential equation)是帶有各種滯後量的微分方程(微分差分方程)、各種具有複雜變元的微分方程、帶有滯後量的積分微分方程等一類方程的概括和...
滯後型泛函微分方程(retarded functional dif-ferential equation)最基本的一類泛函微分方程,即概括各類時滯微分系統的一類泛函微分方程,是泛函微分方程理論的主體...
中立型泛函微分方程(neutral functional dif-ferential equation)最高階導數存在滯後的一類泛函微分方程。...
《時滯微分方程——泛函微分方程引論》是2013年科學出版社出版的圖書。...... 《時滯微分方程——泛函微分方程引論》是2013年科學出版社出版的圖書。書名 時滯微分方...
線性時滯系統是指其微分方程或狀態方程是線性的時滯系統。各種系統中的一些現象,現在的狀態變化率不僅依賴於當前的狀態,還依賴於過去的狀態,系統的這種特性就稱為...
時滯動態系統可由滯後型泛函微分方程描述,其控制系統的分析和綜合設計因涉及無窮極點的問題,所以增加了解決問題的難度。隨著泛函微分方程等相關數學理論的發展完善,以及...
《泛函微分方程的相空間理論及套用》是2009年科學出版社出版的圖書,作者是王克,范猛。...
時滯動力系統(dynamical system with timlag)是泛函微分方程的一類特殊過程。...... 時滯動力系統(dynamical system with timlag)是泛函微分方程的一類特殊過程。...
廣義時滯系統,也稱為廣義微分差分方程,或廣義泛函微分方程。廣義系統是一類形式更一般化,並有著廣泛套用背景的動力系統。自70年代以來,廣義系統理論的研究已經取得了...
在微分方程理論的研究中有重要套用的上下解方法基礎;時滯泛函微分方程基礎理論,以及作者在解的存在惟一性方面和在邊值問題方面的研究成果;非線性差分方程的基本概念...
概念和基本理論,並被表達為各種不同的數學模型,現在主要採用泛函微分方程模型的...非線性時滯系統的鎮定性分析與跟蹤控制理論是系統與控制理論的兩個重要的研究方向...
小時滯等價命題(equivalent proposition forsmall delays)是泛函微分方程穩定性理論的重要概念之一。...
研究領域:常(泛函)微分方程、時標動力學方程理論及套用;數學生態學。...9. 李曉月,范猛,王克.具反饋控制和無窮時滯單種群模型周期正解, 高校套用數學...
26. 魏鳳英,Ch空間中無窮時滯隨機泛函微分方程解的存在唯一性,廈門大學學報(自然科學版),2010,49(2):152-156.27. 魏鳳英,Cg空間中無限時滯隨機泛函微分方程解的...
[15]周英告,具無窮時滯泛函微分方程的周期解. 工程數學學報,2007,24(1):111-118;[16]Yinggao Zhou,Xianhua Tang,On existence of periodic solutions of ...
馬萬彪,男,北京科技大學套用數學系教授、博士生導師,屬於泛函微分方程與生物動力系統梯隊,中國數學會生物數學專業委員會 副理事長兼任秘書長,生物數學學報(科學出版社...
8 具有無窮時滯泛函微分方程正周期解的存在性與多解性,東北大學學報,2007,5。9 非線性運算元方程的變號解存在性多解性及其套用,東北大學學報,2007,6。...
8 具有無窮時滯泛函微分方程正周期解的存在性與多解性,東北大學學報,2007,5。 9 非線性運算元方程的變號解存在性多解性及其套用,東北大學學報,2007,6。 10 非線...
8 具有無窮時滯泛函微分方程正周期解的存在性與多解性,東北大學學報,2007,5。9 非線性運算元方程的變號解存在性多解性及其套用,東北大學學報,2007,6。...
代表作有:《Volterra積分微分大系統的穩定性》、《Marchkov漸近穩定定理的改進及其套用》、《無窮時滯泛函微分方程的穩定性》、《中立型泛函微分方程解的有界性》、...
