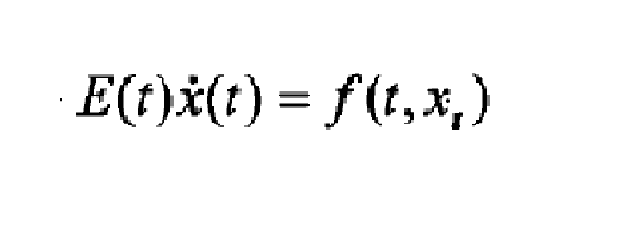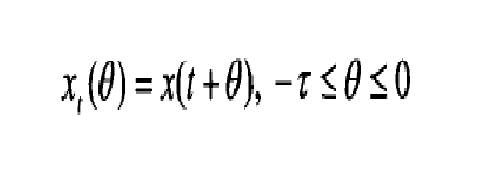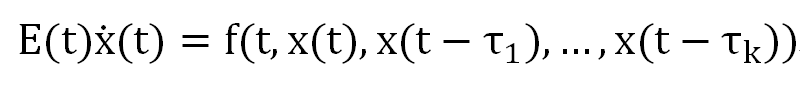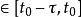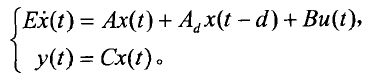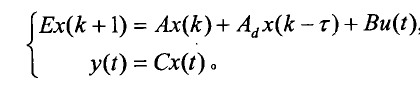廣義時滯系統

廣義時滯系統，也稱為廣義微分差分方程，或廣義泛函微分方程。

廣義系統是一類形式更一般化，並有著廣泛套用背景的動力系統。自70年代以來，廣義系統理論的研究已經取得了長足的進展，許多正常系統的結論被相繼地推廣到廣義系統中。時滯是客觀世界及工程實際中普遍存在的現象，關於時滯系統的研究，近年來也已有非常大的發展。廣義系統中包含了大量帶有時滯的廣義系統，它是比正常時滯系統更加廣泛的一類系統。它產生於電機、經濟中的投入產出、計量經濟、環境污染、宇宙飛船等多種模型中。

基本介紹

• 中文名：廣義時滯系統
• 外文名：Time一delay singular systems
• 提出時間：1980年
• 類別：控制科學與工程
• 套用：電機、計量經濟、環境污染等
• 別名：廣義微分差分方程

背景及發展概況

1750年Euler提出一個古典的幾何學問題：是否存在一種曲線，它經過平移、旋轉運動以後能與其漸縮線重合。1771年，Cnodocret討論這個問題，導出了已知的、歷史上第一個泛函微分方程。此後一個世紀中，許多著名的數學家，如Bemuoh，Lpaacle，Possino以及Bbabege等都提出過類似的方程。鑒於這些類型方程的複雜性，一直未能對它們進行有效地研究，而作為數學的一種歷史懸案擱置下來了，但人們對泛函微分方程已逐漸有所認識。特別是七十年代以後，隨著對諸如管理系統、生態系統、電力系統、工業工程系統等實際系統的建模、設計、分析和套用的深入發展，人們越來越重視時滯現象，並進行了系統的研究，取得了實質的、全面的進展，八十年代以後有了一些有趣的初步結果。

泛函微分方程又稱為病態方程、時滯方程、後效方程、差分微分方程、具有偏差變元的微分方程等。其中時滯是指信號傳輸的延遲，是客觀世界及工程實際中普遍存在的一種物理現象，共同的特點是時滯系統的運動規律不僅與系統當前的運動狀態相關，同時還與過去的運動狀態有關。時滯本質上是無限維的，因而研究具有時滯的系統較為困難，對它的研究也受到廣大學者的關注。

時滯系統具有廣泛的實際背景。本世紀以來，自然科學與社會科學的許多學科中提出了大量時滯動力學系統問題，如核物理學、電路信號系統、生物系統、化工循環系統、遺傳問題、流行病學、動物與植物的循環系統。社會科學方面主要是各種經濟現象時滯的描述，如商業銷售問題、財富分布理論、資本主義經濟周期性危機、運輸調度問題、工業生產管理等。各種工程系統中的時滯現象更為普遍，如流體的傳輸系統、軋鋼系統、機械傳動系統等，特別是自動控制系統。

關於時滯系統和廣義系統的研究，近年來已有非常大的發展。但是這兩方面的研究尚有許多問題需要進一步討論、研究。在許多牢際系統中，要對其準確地描述，從而對其更精確地設計、分析和套用，就必須同時考慮時滯的影響和奇異現象。廣義系統中包含了大量帶有時滯的廣義系統，特別是有代數約束條件的時滯(大)系統及時滯控制(大)系統都是帶時滯的廣義系統。科學技術的迅速發展，又提出了對帶有時滯的廣義系統進行研究。時滯廣義系統是比正常時滯系統更加廣泛的一類系統，在某種條件下，正常時滯系統可以視為時滯廣義系統的一個特例。而且，有些問題只能用時滯廣義系統加以描述，例如，複雜電路網路模型。因此，研究時滯廣義系統，將為科學技術、工程實際提出新的理論方法與解決問題的途徑，具有重要的理論意義和使用價值。

自1993年以來，國內外學者陸續開展了關於時滯廣義系統的研究工作，給出了一系列非常有意義的結果。謝湘生、劉永清等開展了時滯廣義系統的穩定鎮定與控制的研究；謝湘生和劉洪偉給出了時滯廣義系統反饋鎮定控制器設計的線性矩陣不等式方法；而李遠清、劉永清等系統地開展了對時滯廣義系統的基本理論的研究，即解的存在性、唯一性、整體性等，包括將S.L.Campbell關於解的存在唯一性條件中，初始函式及強迫函式的無窮次可微條件降至只要求連續、以及廣義泛函微分方程的研究等，並以著作形式給出總結；溫香彩、李永清、李遠清等對時滯廣義系統的變結構控制、測度型帶有脈衝的時滯廣義系統的穩定性及時滯廣義變結構控制系統解的存在唯一性等進行了研究。蔣威藉助廣義逆陣建立了線性時滯廣義系統的基本理論，進而討論了解的穩定性、周期解的存在性和系統的可控性等問題，得到較為系統的結果。

時滯廣義系統與廣義系統相比，有更為複雜的特性。時滯廣義系統，除了具備時滯系統解不能反向延展、解軌道可以相交、解具有變異性、解空間為無窮維等性質外，它還具有不含時滯的廣義系統的一些複雜特徵及獨特的本質特性與複雜性。

表達方法

如果廣義系統在t時刻狀態的變化率依賴於t和t以前一段時間[t- ,t]上的狀態，則時滯廣義系統可表示為：

其中，E(t)是n階時變矩陣；xt表示由[t- ,t]上的狀態確定的[- ,0]上的函式：

f是t和函式xt的函式，即泛函。

如果系統在t時刻狀態的變化率依賴於t和t以前k個時刻的狀態，則時滯廣義系統可表示為：

這裡，f是一般的多元函式。這時系統在t0時刻的初始狀態表示為：x(t)=(t),t。

特別地，線性時不變連續時滯廣義系統通常表示為：

其中，x(t)，u(t)，y(t)分別是是系統的狀態向量、控制向量及輸出向量；

相應地，線性時不變離散時滯廣義系統表示為：

對不含時滯的廣義系統的初值問題，為使其解存在，初始條件必須是相容的。以線性定常的廣義系統為例，在正則的條件下，若所給的初始條件不相容，則在系統的指數為1的情況下，不相容初始條件會導致初始時刻解的一個“跳躍”。而對線性定常時滯廣義系統，不相容初始條件導致的跳躍就不再像正常的線性定常系統那樣，只限制於初始時刻。經時滯因素的作用，跳躍間斷點將分布到整個時間半軸，以致這樣的初始條件所確定的解成為“振盪”解，振幅與原來初始跳躍的強度有關，而頻率則取決於時滯的大小，時滯越小，頻率越高。這樣略去時滯就無法準確地了解系統解的性態，也說明了時滯廣義系統的複雜性。對這類系統的基本理論、穩定性、控制理論和套用等方面的研究，由於其難度較大，到目前為止研究成果尚不多見。但對時滯廣義系統的研究，將具有十分重要的理論價值和實際意義。

保成本控制

保成本控制 (亦稱保性能控制)問題最早是由Chnag和Pneg在1972年在自適應控制中提出。保成本控制與魯棒控制、最優控制等有著密切的聯繫。現代控制理論、最最佳化方法、統計數學等構成了保成本控制的理論基礎。該方法的一個最大的優點就是，在保證閉環系統魯棒穩定的同時，保證了由於系統的不確定性引起的惡化後的性能指標仍小於事先估計的性能指標上界。這就使得人們對系統性能的惡化程度有了一定程度的了解。基於這一思想，大量學者針對各種系統做了廣泛研究，經過二十年的努力，取得了很多有意義的成果。

1995年首次將保成本控制的概念推廣到不確定時滯系統，通過對參數Riccait方程的求解得到了一個保成本控制器，但Riccati方程的求解十分困難。俞立等人套用線性矩陣不等式研究了一類不確定時滯系統，給出了存在無記憶狀態反饋保成本控制器的充分條件。並且分別給出了狀態反饋最小化保成本控制律的設計方法及利用Lypaunov一Krasovksi函式和一組線性不等式的可行解的基於動態輸出反饋線性時滯系統保成本控制律的設計方法。對離散時滯系統保成本控制問題的研究是通過將離散時滯系統轉化為一個不含時滯的離散系統，從而套用有關離散系統的結果來解決離散時滯系統的分析和綜合的問題。目前對離散時滯系統的保成本控制問題的研究還不是很完善。

套用

時滯廣義系統具有廣泛的實際背景，主要套用於神經網路系統、商品銷售、經濟動態投入產出、環境污染、宇宙飛船航行姿態、電動機速度控制等。