滴定量熱法也稱熱滴定法或測溫滴定法。是一種量熱或分析技術，即用一種反應物滴定另一種反應物，隨著加入滴定劑的數量的變化，測量反應體系溫度的變化。
滴定一般在儘可能接近絕熱的條件下進行，被滴定物可以是液體或懸浮的固體；滴定劑可以是液體或氣體。溫度變化是由滴定劑與被滴定物間的化學作用或物理作用（例如一種有機分子吸附於固體表面）引起的。
實驗數據以熱譜圖形式表示，它提供了有關反應中物質的量（滴定終點）和反應物質的特性（焓變）的數據。對圖進行分析，可以得知反應容器中發生的反應的類型和數目，以及溶液中存在的各物種的濃度等信息。這部分內容稱為熱滴定，同時還可以確定反應的化學計量關係，計算反應的熱力學量,如平衡常數K(ΔG°)、標準狀態下的焓變ΔH°和熵變ΔS°,這部分內容稱為滴定量熱法。
測溫滴定法以熱效應為基礎,與溶液的許多性質(如粘度、光學透明度、介電常數、溶劑強度、以及離子強度等)無關,因此可以用於氣相、液相、非水溶液、有色溶液、膠體溶液和粘稠漿狀等體系。
基本介紹
- 中文名：滴定量熱法
- 外文名：isothermal titration calorimetry
- 發明者：P.迪圖瓦和E.格羅貝特
- 發明時間：1922年
- 學科：物理熱力學
簡史,裝置,類型,套用,
簡史
1922年P.迪圖瓦和E.格羅貝特建立熱滴定法，用於容量分析。1924年P.M.迪安和O.O.瓦茨最早使用測溫滴定這一術語；以後又有人採用熱滴定、焓滴定、測溫焓滴定、量熱滴定和測溫滴定等術語，至今仍未統一。
70年代以來,由於與滴定量熱計相關的一些技術(如恆溫浴、恆速滴定裝置、反應容器、溫度感測電路以及數據分析手段等)獲得迅速發展,連續滴定法結果的精度已可與常用溶液量熱計比美，而且能夠滴定少於毫克級的試樣。因此熱滴定不僅可用於分析目的，而且已成為一種精密量熱技術。滴定量熱法特別適用於下述目的：在有連串反應或並行反應存在的情況下，測定焓變ΔH；用於包含微弱相互作用物種的反應，求吉布斯函式改變ΔG；鑒別絡合反應中存在的物種等。還用於測定混合熱、物質在兩相中的分配係數和吸附容量等，並可用於生物化學、微生物學和環境化學等方面。
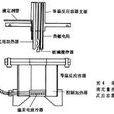
裝置
圖1為滴定量熱計框圖。滴定管內含有一種反應物的滴定劑，可加入到反應容器內，滴定劑的濃度一般為被滴定液的數十倍甚至一百倍左右。反應產生的溫度變化由溫度感測器（例如熱敏電阻）感知，通過惠斯通電橋電路轉換為相應的伏特數或熱功率。這個伏特數由放大電路放大並記錄於記錄儀上，或者饋入其他的數據採集系統。反應容器和滴定管置於同一恆溫浴中，恆溫浴溫度由溫度控制器控制，並由溫度感測器測量。滴定劑和反應容器的溫度必須相等，或者它們之間的溫差必須精確知道。
滴定劑的加入方式 ①連續加入法：滴定劑以恆速加入，可以得到滴定進程中熱效應的完整記錄。對於特別複雜的反應，可以從這種記錄圖中選擇任意數目的數據點，用於必要的計算。連續滴定法要求對溫度變化的回響必須夠快，並且此法只適用於快速反應。②分次遞增加入法：間歇地每次加入單位增量的滴定劑，在每次加入單位增量前，必須調節反應容器的溫度，使回復到起始溫度，通過加入許多次增量，也能夠得到足夠的測量數據，從而繪製成與連續法相似的圖線。不過，它比連續法的工作量要大一些。遞增法的好處是可以精確研究動力學上較慢的反應。③連續流動量焓法：使兩種溶液各自以恆速連續流過一個混合(測量)容器。此法的優點是反應物於不存在氣相情況下混合，這對於測量揮發性液體體系非常重要，並且可以忽略表面吸附效應。該法特別適用於研究複雜的生物化學和微生物學過程。此外，此法的裝置可以連線在生產線中進行分析而達到過程控制的目的。
類型
①環境等溫式：將反應容器浸沒於恆溫浴中，連續監測反應容器內溫度隨著滴定劑加入量的變化；②等溫式：實驗中維持反應容器和器內物（即體系）的溫度恆定,並且嚴格等於其環境的溫度,同時監測流過反應容器的熱量變化。在滴定中，熱量變化僅僅來源於容器內滴定劑與被滴定物的物理或化學變化。等溫法比環境等溫法優異之處是不需要進行體系與環境之間的熱交換改正。
滴定量熱法包含這樣的假定，即測得的數據表示量熱計系統既達到了熱平衡，也達到化學平衡的結果。當然，實際上達到精確的熱平衡是十分困難的。目前環境等溫式滴定反應容器已可達到的熱平衡時間約為2秒;等溫式的容器情況更好。環境等溫式滴定量熱計反應容器的設計,應該使其與環境之間的熱交換為最小。圖2是一種典型的滴定反應容器。由於杜瓦容器的玻璃內壁很薄,其內部各部件(攪拌器、熱敏電阻、加熱器等)的質量都很小,所以這種設計有利於迅速建立熱平衡。
右圖為一種等溫滴定量熱計框圖。這種方法的原理可以簡單地歸結為：用溫差電致冷器恆速冷卻，而用一個可調加熱器的焦耳熱進行補償調節。對於放熱反應,反應的熱功率q等於以熱功率表示的致冷量qc與焦耳熱的熱功率qh之差;對於吸熱反應,則q為qh與qc之差。實驗中qc的數值始終維持不變，而qh的大小則視是吸熱或放熱反應以及反應熱功率q的大小而不斷調節。因此，qh的變化也就是q的變化值。
利用這種方法，可使體系中附加熱效應（如攪拌熱、熱敏電阻自熱）預先得到抵消。即在加入滴定劑的過程中，調節qh的大小，使得反應熱效應得到補償。實驗過程中，始終維持體系與環境溫度嚴格相等。目前這種型式的量熱計中,反應容器的溫差不超過5×10-6℃。這種量熱計的基本結構如圖4所示。
測溫滴定法 是以反應熱為基礎的滴定方法，用於分析化學時，熱效應的利用可分為兩種方式：①測溫焓滴定，即利用反應熱確定反應終點。在滴定過程中，試樣的溫度作為加入滴定劑體積的函式進行測量。②直接注射法測焓技術,根據反應熱確定滴定劑的加入量,即把滴定過程的總熱量與該反應的已知摩爾熱進行比較。測溫滴定法已經得到普遍套用。無論是酸鹼滴定法、沉澱滴定法、氧化還原滴定法或者絡合滴定法，只要能觀測到足夠的溫度升高，都可以套用。另外，測溫滴定的動力學特性也值得重視。例如，當混合物中的兩個組分與滴定劑的反應速率相差很大時，就有可能逐次把兩個組分滴定出來；又如，一個有催化劑與一個無催化劑的體系，滴定時是有差異的，這種差異也可資利用。 圖5為放熱反應的理想滴定曲線。E為滴定終點，DD′為溫度升高。在實際過程中，滴定曲線在終點附近往往會出現彎曲的現象，如圖6所示。引起彎曲的原因有二:一是反應的平衡常數K值小(K<104),反應不完全；二是這種彎曲也可由緩慢反應引起。如果終點區變彎只是由於K值小而引起的,則為了得到滴定終點,可將曲線外延(圖6b)。不過,當外延部分超過反應區的一半時，實驗結果會失去意義。
套用
滴定量熱法在量熱學中是測定熱力學函式的有效手段，例如測定焓變ΔH。圖7是連續量熱滴定得到的典型圖譜。圖中從 D點開始加入滴定劑,P點代表至此點前加入的滴定劑總量所對應的表觀總熱效應。滴定曲線在圖上分為a、b、d三個區段。a段為熱實驗初期,圖線的斜率與攪拌熱、熱敏電阻自熱和熱漏值的大小有關；b段是滴定期即實驗主期，熱效應包括反應熱和稀釋熱、在 D點處滴定劑與被滴定物二者之間的溫差效應以及a段的各種熱效應；d段為實驗末期，此時已停止加入滴定劑，這段圖線的斜率所受影響與a段相同,只是反應容器內溶液的體積變大了。在這種情況下，在將滴定劑加入滴定液的過程中，有可能發生一個或多個反應。各個反應進行的程度和產生的熱效應與該反應的平衡常數K和反應的焓變有關。把熱效應、K和ΔH聯繫起來的公式一般是複雜的。如果容器中總共包含n個反應，則這些量之間的關係可以表示為：
(1)QC,P是從滴定開始點D到P點間容器中的n個反應的總熱效應；Δni,P是從D到P之間第i個反應產物生成的摩爾數，它與該反應的平衡常數有關；ΔHi為該反應的焓變。ΔHi的最佳值一般可通過對式 (1)進行最小二乘方分析處理得到，即對m個數據點的測量誤差的平方和s為：
(2)P表示包括所有的數據點；i表示包括所有的反應。運行一次測試 (得一個熱譜圖) 的 ΔHi最佳值應是使s(ΔHi,Ki)最小的ΔH值，因此：
(3)式中k=1,2,3,…,n,實際上式(3)有n個方程，各為ΔHi(i=1,2,3,…,n)的一次方程。如要各個反應的平衡常數ki為已知,則Δni的值也已知，就可以解出各個ΔHi的最佳值。
滴定量熱法的另一用途是計算K值。套用量熱法確定體系的平衡常數必須滿足以下條件:①K值和反應物種的濃度必須在一定範圍內(約為104<K<10)以保證熱譜圖有充分的彎曲度；②該反應的ΔH值足夠大，使得測量出來的總熱效應數值的重複性優於0.5%(更精確的數據要求重複性優於0.2%，此時溫度變化值至少為0.01℃)。這些限制似乎較苛刻，實際上對於有些體系，如質子電離作用和金屬配位體相互作用等，選擇使用適宜的滴定劑可以測定任意大小的K值。由K和 ΔH值可以得到反應的標準吉布斯函式變化ΔG°和熵變ΔS°：
ΔG°=－RTlnK
ΔS°=(ΔH°－ΔG°)/T
