混合張量(mixed tensor)是一類張量。向量空間及其對偶空間張量積的元素。張量是向量概念的綜合,可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力聯繫起來。張量計算最初的發展是與微分幾何相聯繫的,也是愛因斯坦在系統地闡述廣義相對論時所用的基本工具。
基本介紹
- 中文名:混合張量
- 外文名:mixed tensor
- 領域:數學
- 性質:張量
- 空間:向量空間及其對偶空間
- 套用:微分幾何、黎曼幾何
概念

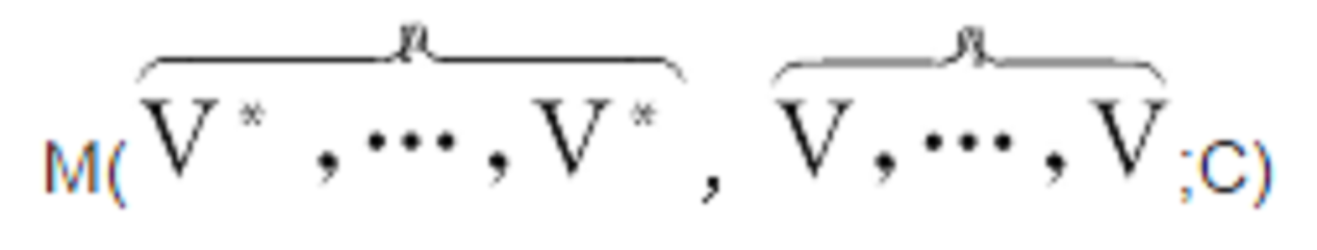
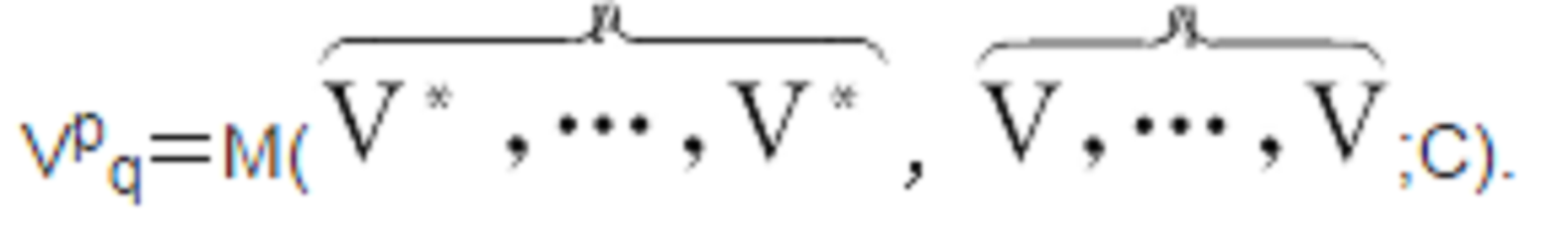
張量

向量空間








混合張量(mixed tensor)是一類張量。向量空間及其對偶空間張量積的元素。張量是向量概念的綜合,可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力聯繫起來。張量計算最初的發展是與微分幾何相聯繫的,也是愛因斯坦在系統地闡述廣義相對論時所用的基本工具。

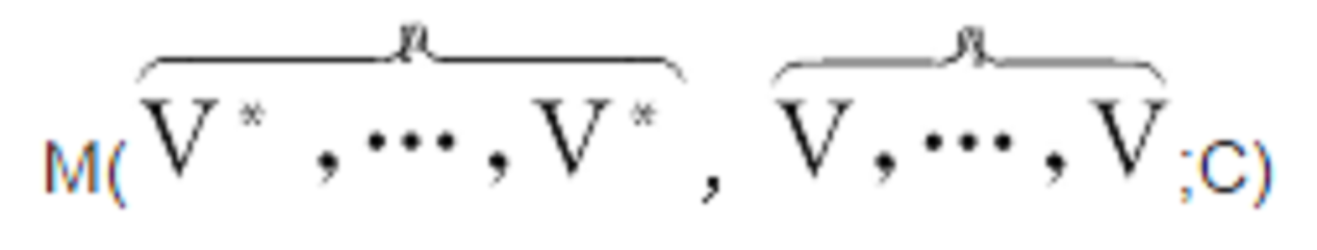
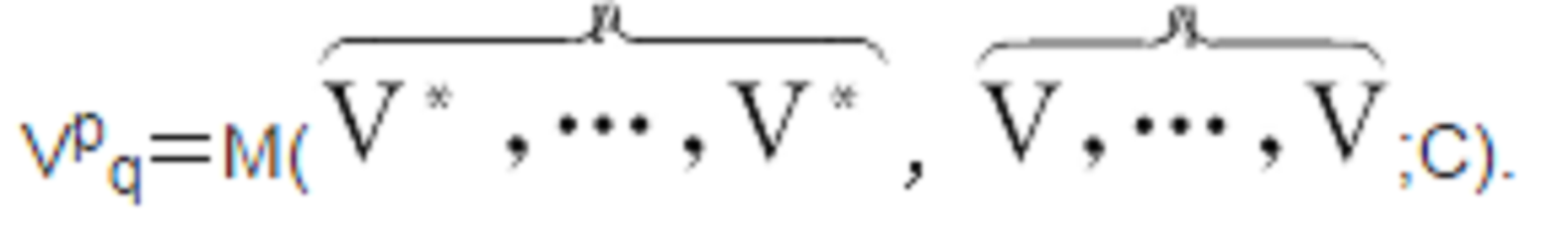








混合張量(mixed tensor)是一類張量。向量空間及其對偶空間張量積的元素。張量是向量概念的綜合,可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力聯繫起來。張量計算最初的發展是與微分幾何相聯繫...
稱為r階逆變和s階協變混合張量的分量。若s=0,則 稱為r階逆變張量的分量。若r=0,則 稱為s階協變張量的分量。上述這種張量記法稱為分量記法。2.按不變性定義 凡可以在任何坐標系中寫成下列不變性形式的量定義為r+s階張量...
張量映射(tensorial mapping)混合張量代數中的一類線性映射.設E*,E是域K上的對偶空間,dim E=n , a是E的自同構.對每對(p,婦都確定岡$(E* ,E)的線性自同構To。定義介紹 ,它由 給出,其中滬}ao分別為a在②E' ,②E上的...
協變張量(covariant tensor)是指所有指標都是協變指標的張量。既有協變又有逆變的張量為混合張量。(協變)張量的定義 坐標系的變換關係 僅討論笛卡兒右手直角坐標系。舊坐標系: 單位基矢量: ;新坐標系: 單位基矢量: ,如圖1...
每項是一個張量外乘(或內乘)另一張量的協變導數。不變微分運算元 梯度 散度 旋度 拉普拉斯運算元 內稟微分 絕對導數 實質導數 相對張量 權為w的相對純量 權為w的相對矢量 權為w的相對二階混合張量 權為1的相對張量 (張量密度)
張量源混合電磁法(tensor-source magnetotelluric method)是一種類似可控源音頻大地電磁法的勘查技術。在這裡,發射源是由兩個交錯放置的獨立極化的電流偶極子組成的,在測點上則觀測對應於每個獨立源的電磁場分量,而相應於每個頻點的平面...
第1章矢量與張量1 1.1矢量及其代數運算公式1 1.1.1矢量1 1.1.2點積2 1.1.3叉積2 1.1.4混合積3 1.2斜角直線坐標系的基矢量與矢量分量5 1.2.1平面內的斜角直線坐標系5 1.2.2三維空間中的斜角直線坐標系7 1.2.2....
1.3 坐標變換與基變換 1.4 張量(tansor)1.5 張量的實體表示 1.6 度量張量 1.7 矢量的叉積、混合積和置換張量 1.8 Ricci符號和行列式 1.9 張量的代數運算 1.10 例題 習題一 2 張量場論 2.1 引言 ...
)”則相對容易理解,作者以此為起點,分為六個部分,二十個章節,一步步向讀者介紹,直至張量。如:第一部分從矢量的袋鼠運算講起,詳述矢量的矢量混合積;第二部分,引入矢量三重系;第三部分,先講解變矢量的微分運算;第四部分,...
第1章矢量和張量(1)1.1矢量及其代數運算(1)1.1.1矢量和(2)1.1.2矢量的點積(3)1.1.3矢量的叉積(3)1.1.4矢量的混合積(4)1.1.5矢量的三重叉積(5)1.2微分運算元(6)1.3坐標系及基矢(11)1.3.1直角坐標系(11)1....
由於語音在時域體現出高階線性卷積混合形式,難以直接求解,頻域語音分離得到了越來越多的關注。特別地,隨著張量等高維數學工具越來越多地被套用至盲源分離之中,基於張量分解的頻域語音分離成為近些年來的研究熱點。頻域語音分離在關鍵在於...
由模的張量積構造的一類代數。或者是各階反變張量空間的並構成的代數。混合外代數(mixed exterior algebra)是外代數的推廣。概念介紹 混合外代數(mixed exterior algebra)外代數的推廣。設E*,E是特徵為零的域K上的對偶空間,∧E*,∧...
C6係數和外積約化係數的方法、線性Lie群的混合張量表示和它的套用,以及用Schur函式方法導出經典Lie群的分支規則等方面的系統討論作為一本書的內容尚屬首次。後兩章介紹群論在核物理中的套用,特別介紹了廣義相干態的套用;在此,我們還...
第一篇 張量 第二章 張量積 2.1 雙線性映射和張量積 2.2 張量積的存在性 2.3 線性映射的張量積 2.4 張量積的另一種構造方式 2.5 正合序列 2.6 混合張量 習題 第三章 張量代數 3.1 代數 3.2 對稱群 3.3 張量代數 3....
walled Brauer (超)代數與一般線性李超代數(Q-型李超代數)之間的 super Schur-Weyl 對偶,確定和構造了Kac-模與自然表示的混合張量模的最高權向量;引進了例外型李超代數的 Jantzen 濾過;定義了李超代數新的上同調理論,即混合上...
稱為愛因斯坦張量, 是從黎曼張量縮並而成的里奇張量, 是從里奇張量縮並而成的曲率標量 是度規張量; 是能動張量,G是萬有引力常數,c是真空中光速。愛因斯坦場方程是一組含有若干2階對稱張量的張量方程。每一個張量都有10個獨立的...
第1章 向量和張量基礎 1 1.1 向量的基本概念和表示 1 1.2 向量的基本代數運算 2 1.2.1 點積(內積) 2 1.2.2 叉積(外積) 3 1.2.3 混合積 4 1.2.4 張量積(並矢) 4 1.3 二維空間中非正交直線坐標系下的向量表示 ...
高階彈性常數,研究報導的最高彈性常數為6階彈性常數,大部分超硬材料的高階彈性常數仍然是未知的。導論 眾所周知的是二階彈性常數是一個二階四秩張量(cijkl),三階彈性常數是三階六秩張量(Cijklmn);更高階的彈性常數還包括四...
這樣,對應於每一個分力Fx、Fy、Fz、以作用於Ax、Ay、Az三個互相垂直的面,應力F/A有九個不同的分量,因此嚴格地說應力是一個張量。由於流體不能產生切變,不存在切應力。因此對於靜止流體,不管力是如何作用,只存在垂直於接觸面的...
[53] 馮遠靜, 吳燁, 許優優, 單敏, 李蓉, 李志娟, 王哲進, 高成峰, 葉峰, 陳蒙奇, 李斐. 用於腦白質纖維跟蹤的高階擴散張量混合稀疏成像方法(授權號:ZL201410558017.9)發明專利。軟體著作權登記 [54] 吳燁,馮遠靜,高成鋒...
隨後,我們證明了有限維單李超代數上的Hom-李超代數結構的平凡性。給出了一般線性單李超代數通過非齊次多項式表示利用混合積張量的表示的合成列,並給出了在這個合成列中出現的不可約模(這些不可約模都是最低權模)的特徵標公式。
第1章 向量和張量基礎 1 1.1 向量的基本概念和表示 1 1.2 向量的基本代數運算 2 1.2.1 點積(內積) 2 1.2.2 叉積(外積) 3 1.2.3 混合積 4 1.2.4 張量積(並矢) 4 1.3 二維空間中非正交直線坐標系下的向量表示 ...
