基本介紹
- 中文名:泛中心擴張
- 外文名:universal central extension
- 所屬學科:數學
- 相關概念:中心擴張、同態、同構等
定義,K2群的泛中心擴張刻畫,李Poisson超代數的泛中心擴張,
定義
泛中心擴張是指群的一類特殊的中心擴張,設 為群的滿同態,若核
為群的滿同態,若核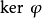 在G的中心中,φ就稱為H的中心擴張,也稱G為H的中心擴張。若中心擴張φ又滿足如下的泛性質:任給H的中心擴張
在G的中心中,φ就稱為H的中心擴張,也稱G為H的中心擴張。若中心擴張φ又滿足如下的泛性質:任給H的中心擴張 ,都有惟一的群同態
,都有惟一的群同態 使
使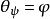 ,則稱φ為H的泛中心擴張。在同構意義下,H只能有一個泛中心擴張,泛中心擴張不但在群論中是一個重要概念,在代數K理論中特別是在K2群的理論中具有重要意義。
,則稱φ為H的泛中心擴張。在同構意義下,H只能有一個泛中心擴張,泛中心擴張不但在群論中是一個重要概念,在代數K理論中特別是在K2群的理論中具有重要意義。

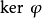


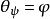
K2群的泛中心擴張刻畫
命題1 (1) 群G有泛中心擴張 G為完全群,即G=[G,G](例如非Abel單群);
G為完全群,即G=[G,G](例如非Abel單群);

(2) 群G的中心擴張 為泛中心擴張
為泛中心擴張 下兩條成立:
下兩條成立:


(i)E為完全群;
(3)若G為完全群,



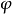

推論1 群G有完全中心擴張 (即滿足
(即滿足 的中心擴張
的中心擴張 )
)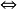 G有泛中心擴張。
G有泛中心擴張。



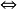
定理 設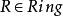 ,則
,則 ,因此
,因此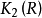 為E(R)的泛中心擴張之核。
為E(R)的泛中心擴張之核。
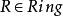

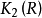
李Poisson超代數的泛中心擴張
定義1設T是域F上李Poisson超代數,如果 則稱T是完全的。
則稱T是完全的。

定義2 設T是域F上李Poisson超代數, 為李Poisson超代數T的中心。
為李Poisson超代數T的中心。

定義4 設 是李Poisson超代數T的中心擴張,若對T的任意中心擴張
是李Poisson超代數T的中心擴張,若對T的任意中心擴張 ,都存在唯一的李Poisson超代數同態
,都存在唯一的李Poisson超代數同態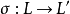 ,使得
,使得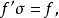 則稱
則稱 是T的泛中心擴張;如果
是T的泛中心擴張;如果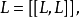 則稱此擴張為T的泛覆蓋。
則稱此擴張為T的泛覆蓋。


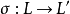
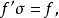

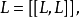
引理1 若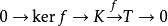 與
與 均為T的泛中心擴張,則
均為T的泛中心擴張,則 。
。
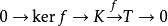


定理1 設 是李Poisson超代數T的泛中心擴張,則T完全的充要條件是L 完全。
是李Poisson超代數T的泛中心擴張,則T完全的充要條件是L 完全。

定理2 如果T是完全李Poisson 超代數,則 是李Poisson超代數T的泛中心擴張,且
是李Poisson超代數T的泛中心擴張,且 也是完全的。
也是完全的。


定理3李Poisson超代數T存在泛覆蓋若且唯若T是完全的。
推論1設 分別是李Poisson超代數K和T中心擴張,則
分別是李Poisson超代數K和T中心擴張,則 是T的泛中心擴張若且唯若
是T的泛中心擴張若且唯若 是K 的泛中心擴張。
是K 的泛中心擴張。



為了研究問題的方便,不妨設上面所構造出來T的泛中心擴張函式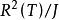 為
為 。
。
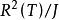

定理4設T和T'均是李Poisson超代數,且T 完全,則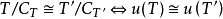 。
。