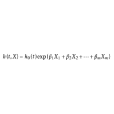COX回歸模型，又稱“比例風險回歸模型(proportional hazards model，簡稱Cox模型)”，是由英國統計學家D.R.Cox(1972)年提出的一種半參數回歸模型。該模型以生存結局和生存時間為因變數，可同時分析眾多因素對生存期的影響，能分析帶有截尾生存時間的資料，且不要求估計資料的生存分布類型。由於上述優良性質，該模型自問世以來，在醫學隨訪研究中得到廣泛的套用，是迄今生存分析中套用最多的多因素分析方法。
基本介紹
- 中文名：COX回歸模型
- 外文名：Cox regression model
- 全稱：Cox比例風險回歸模型
- 提出人：D.R.Cox
- 簡稱：Cox模型
基本概念,基本原理,假設檢驗,相關事件,
基本概念
在介紹Cox回歸模型之前，先介紹幾個有關的概念。
1.生存函式具有變數
的觀察對象的生存時間
大於某時刻
的機率，
2. 死亡函式具有變數
的觀察對象的生存時間不大於某時刻的機率，
3. 死亡密度函式具有變數X的觀察對象在某時刻t的瞬時死亡率，稱為死亡密度函式。
4. 危險率(風險)函式具有變數X，且生存時間已達到的觀察對象在時刻的瞬時死亡率，
基本原理
生存分析的主要目的在於研究變數X與觀察結果即生存函式(累積生存率)
之間的關係。當 受很多因素影響，即
為向量時，傳統的方法是考慮回歸方程——即諸變數
對 的影響。但由於生存分析研究中的數據包含刪失數據。且時間變數t通常不滿足常態分配和方差齊性的要求，這就造成了用一般的回歸方法研究上述關係的困難。
Cox回歸模型的基本形式
D.R.Cox提出了Cox比例風險回歸模型，它不是直接考察 與X的關係，而是用
作為因變數，模型的基本形式為：
由於Cox回歸模型對
未作任何假定，因此Cox回歸模型在處理問題時具有較大的靈活性；另一方面，在許多情況下，我們只需估計出參數
(如因素分析等)，即使在 未知的情況下，仍可估計出參數 。這就是說，Cox回歸模型由於含有 ，因此它不是完全的參數模型，但仍可根據公式(1)作出參數 的估計，故Cox回歸模型屬於半參數模型。
公式(1)可以轉化為：
Cox回歸模型的假定
1. 比例風險假定 各危險因素的作用不隨時間的變化而變化，即
不隨時間的變化而變化。因此，公式(1)又稱為比例風險率模型(PH Model)。這一假定是建立Cox回歸模型的前提條件。
2．對數線性假定 模型中的協變數應與對數風險比呈線性關係，如公式(2)。
Cox回歸模型中偏回歸係數的意義
由公式(2)可見，模型中偏回歸係數
的流行病學含義是在其他協變數不變的情況下，協變數
每增加一個測定單位時所引起的相對危險度的自然對數的改變數。即
式中，
分別表示在不同情況下的取值。當協變數 分別取1和0時，其對應的
為
從公式(1)和公式(4)可以看出有如下關係：
若
，則各
取值越大時， 的值越大，即 為危險因素。
若
，則各 的取值對 的值沒有影響，即 為無關因素。
若
，則各 取值越大時， 的值越小，即 為保護因素。
假設檢驗
Cox回歸模型中的偏回歸係數可以通過建立偏似然函式，利用Newton-Raphson疊代法求得。其他自變數不變的情況下，變數 每增加一個單位，相對危險度 的
可信區間為：
式中
為的標準誤。
對於回歸模型的假設檢驗通常採用似然比檢驗、Wald檢驗和記分檢驗，其檢驗統計量均服從
分布，其自由度為模型中待檢驗的自變數個數。一般說來，Cox回歸係數的估計和模型的假設檢驗計算量較大，通常需利用計算機來完成相應的計算。
相關事件
提出“COX回歸模型”的著名統計學家David Cox去世。
