基本介紹
- 中文名:正弦積分
- 外文名:sine integral
- 定義:由積分定義的一種特殊函式
- 功能:計算正弦積分函式值
定義

正弦積分函式表

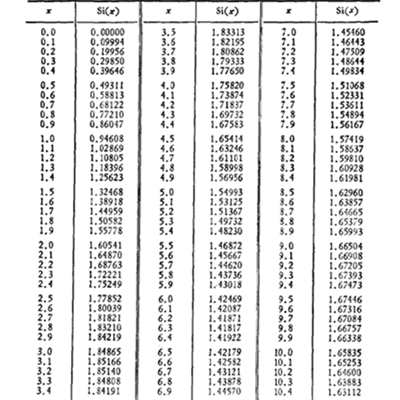
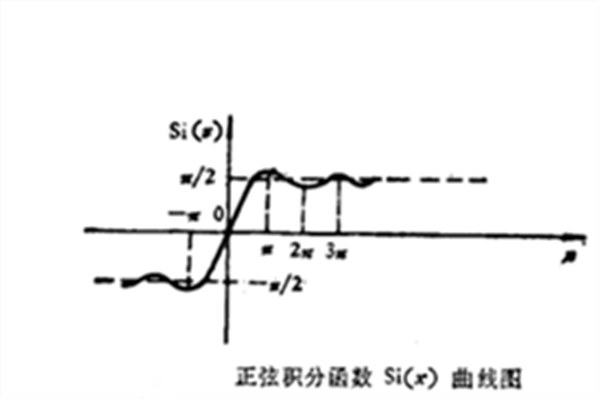
正弦積分函式圖像






正弦積分的計算

























正弦積分是由積分定義的一種特殊函式。英文翻譯為sine integral,常用於計算正弦積分函式值,在性質上常與餘弦積分作比較。定義正弦積分函式的定義為:,本函式採用勒讓德-高斯求積公式計算該積分。正弦積分函式表,函式表...
1.正弦積分 有兩種不同的正弦積分: 是 的原函式,當 時為零; 是 的原函式,當 時為零。我們有:注意到 是sinc函式,也是第零個球貝塞爾函式。2.餘弦積分 餘弦積分定義為:兩者將的關係式為:其中 是歐拉-馬歇羅尼...
由於正弦的導數是餘弦,餘弦的導數是負的正弦,因此正弦函式滿足微分方程:這就是正弦的微分方程定義。正弦積分 恆等變換 用其他三角函式的表示 兩角和的正弦 二倍角公式 三倍角公式 半角公式 和差化積公式 萬能公式 數學術語 正弦函式...
任意銳角的正弦值等於它的餘角的餘弦值,任意銳角的餘弦值等於它的餘角的正弦值,通常用符號sin表示。正弦sinθ也可以理解為頂角度數為θ的單位等腰三角形與單位等腰直角三角形的面積之比。sin30°=1╱2 sin45°=√2╱2 sin60°=√...
包括伽馬函式、ψ函式、黎曼ζ函式、指數積分、正弦積分函式和餘弦積分函式、積分雙曲正弦和餘弦、機率積分、菲涅耳積分、不接近伽馬函式、拋物柱面函式、貝塞爾函式、諾依曼函式等;第3章為多重積分,包括二重積分、三重積分等;第4章為...
積分電路還可以用於處理模擬信號。當輸入為正弦信號 u(t)=Um 時,積分電路的輸出為 u₀(t)=1/RCdt=Um/ωRC 其幅度為輸入信號的1/ωRC,相位落後90°。當輸入信號含有不同頻率分量時,積分電路輸出端的信號中頻率較高的分量...
正弦函式:y=sinx;餘弦函式:y=cosx;正切函式:y=tgx;餘切函式:y=ctgx;正割函式:y=secx;餘割函式:y=cscx.下面分別結合函式的圖形來討論它們的性質。正弦函式:y=sinx與餘弦函式:y=cosx:下面是正弦函式和餘弦函式的圖形:可以...
正弦積分函式與餘弦積分函式 正弦積分函式(Sine Integral Function)與餘弦積分函式(Cosine Integral Function)分別為 和 這兩個函式與指數積分的關係如下 由此可得 這兩個函式的漸近值為 和 指數積分與其它函式的關係 與對數積分 指數...
當一個非常複雜的函式變成多個初等正弦函式相加時,它的積分比之前對複雜函式的積分變得簡單多了。法國數學家傅立葉發現了周期函式可以用一系列正弦函式組成的級數表示。先把函式作傅立葉變換,然後再利用萊布尼茨公式即可求出結果。概念 傅...
的周期T= 1/f ,也就是說合成信號是頻率與基波相同的非正弦信號。3. 正弦信號對時間的微分與積分仍然是同頻率的正弦信號。以上這些優點給運算帶來了許多方便,因而正弦信號在實際中作為典型信號或測試信號而獲得廣泛套用。
(3)輸入正弦信號,用毫伏表測量輸入Ui、輸出Uo幅值。(4)輸入方波信號,用示波器觀測Ui和Uo輸出波形並畫出其方波和三角波電壓波形圖(電壓值、周期)。二、設計性實驗 1、實驗目的 通過積分運算電路設計性實驗,學會簡單積 分電路的...
正弦波振盪器是指不需要輸入信號控制就能自動地將直流電轉換為特定頻率和振幅的正弦交變電壓(電流)的電路。簡介 定義 它由四部分組成:放大電路,選頻網路,反饋網路和穩幅電路。常用的正弦波振盪器有電容反饋振盪器和電感反饋振盪器兩種。
Ⅰ.1 初等函式的不定積分 Ⅰ.2 特殊函式的不定積分 Ⅱ 定積分表 Ⅱ.1 初等函式的定積分 Ⅱ.2 特殊函式的定積分 Ⅲ 積分變換表 Ⅲ.1 拉普拉斯(Laplace)變換 Ⅲ.2 傅立葉(Fourier)變換 Ⅲ.3 傅立葉(Fourier)正弦變換 ...
正弦定理:a/sinA=b/sinB=c/sinC=2R 得 (sinA)^2+(sinB)^2-(sinC)^2-2sinAsinBcosC=0 轉化 1-(cosA)^2+1-(cosB)^2-[1-(cosC)^2]-2sinAsinBcosC=0 即 (cosA)^2+(cosB)^2-(cosC)^2+2sinAsinBcosC...
在積分 中,我們可以用以下的代換:這樣積分變為:注意以上的步驟需要 a > 0和cos(θ) > 0;我們可以選擇a為a2的算術平方根,然後用[[反正弦]]函式把''θ''限制為−π/2 < ''θ'' < π/2。對於定積分的計算,我們...
(2)任何兩個頻率不同的正弦波都是正交的。如果將兩個正弦波相乘並在整個時間軸上求積分,則積分值為零。這說明可以將不同的頻率分量相互分離開。(3)正弦波有精確的數學定義。(4)正弦波及其微分值處處存在,沒有上下邊界。使用...
頻域微積分 微分性質:若 ,則 ;積分性質:若 ,則 。套用 儘管最初傅立葉分析是作為熱過程的解析分析的工具,但是其思想方法仍然具有典型的還原論和分析主義的特徵。"任意"的函式通過一定的分解,都能夠表示為正弦函式的線性組合的...
分析正弦穩態電路的一種方法。1893年由德國人C.P.施泰因梅茨首先提出。此法是用稱為相量的複數來代表正弦量,將描述正弦穩態電路的微分(積分)方程變換成複數代數方程,從而在較大的程度上簡化了電路的分析和計算。在進行分析電路的...
16·10 積分變換簡表 第十七章 特殊函式 17·1 Γ函式 17·2 B函式 17·3 誤差函式.菲涅耳積分 17·4 指數積分.對數積分.正弦積分.餘弦積分 17·5 勒讓德函式.勒讓德多項式 17·6 貝塞爾函式 17·7 埃爾米特函式與埃爾米特...
正弦函式 lymphatic sinusoid 淋巴竇 sinusoid endothelium 竇狀隙內皮 sinusoid sinusoidal 正弦曲線 Complex sinusoid 復正弦曲線 hepatic sinusoid 肝血竇 ; 肝竇 half sinusoid 半正弦波 ; 半正弦曲線 sinusoid integrator 正弦積分器 ...
半角公式(Half angle formula)是利用某個角(如∠A)的正弦值、餘弦值、正切值,及其他三角函式值,來求其半角的正弦值,餘弦值,正切值,及其他三角函式值的公式。公式 常用的半角公式包括以下三個:半角正弦公式 半角餘弦公式 半角...
正弦函式的導數 假設正弦函式y=sin x(x的單位為弧度)上有一點(x,y)和另一點(x+δx,y+δy):d/dx(sin x)=limδx→0 δy/δx =limδx→0 [sin (x+δx)-sin x]/δx =limδx→0 2[cos 0.5(2x+δx)][...
第1章 電磁場的積分公式 1.1 靜電場的積分公式 1.2 恆定磁場的積分公式 1.3 正弦時變電磁場的積分公式 思考題1 第2章 電磁場邊值問題的微分方程 2.1 靜電場的邊值問題 2.2 恆定電流場的邊值問題 2.3 恆定磁場的邊值...
是周期信號瞬時幅值隨時間重複變化的信號。常見的周期信號有:正弦信號、脈衝信號以及它們的整流、微分、積分等 信號分類 常見的周期信號有:正弦信號、脈衝信號以及它們的整流、微分、積分等。這類可稱為簡單信號。它們的特點是在一個周期...
