基本介紹
- 中文名:歐拉數
- 外文名:Euler Number
- 釋義:空洞區域內空洞數量的度量
- 描述方式:一個單一的數
- 命名:萊昂哈德·歐拉
- 學科:線性代數、拓撲學、流體力學
人物介紹
拓撲學中

線性代數中
數學中
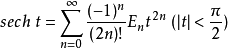
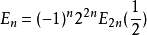
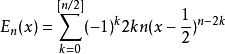

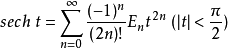
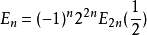
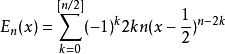
歐拉數(Euler Number)是一個工程中常見的參數,以瑞士數學家萊昂哈德·歐拉(Leonhard Euler ,1707年4月15日~1783年9月18日)的名字命名。其具體意義在不同的學科...
歐拉常數約為e ≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274。歐拉...
在任何一個規則球面地圖上,用 R記區域個 數,V記頂點個數 ,E記邊界個數 ,則 R+ V- E= 2,這就是歐拉定理 ,它於 1640年由 Descartes首先給出證明 ,後來...
在代數拓撲中,歐拉示性數(Euler characteristic)是一個拓撲不變數(事實上,是同倫不變數),對於一大類拓撲空間有定義。...
北京歐拉數術科技有限公司於2014年02月17日成立。法定代表人薄琥,公司經營範圍包括:技術推廣服務;計算機信息系統集成;施工總承包;數據處理(數據處理和存儲服務中銀行...
在數論,對正整數n,歐拉函式是小於n的正整數中與n互質的數的數目(φ(1)=1)。此函式以其首名研究者歐拉命名(Euler's totient function),它又稱為Euler's ...
歐拉準則或稱為壓力相似準則,即兩個流動的慣性力和流體動壓力成比例,則它們的歐拉數相等。...
V+F-E=X(P),V是多面體P的頂點個數,F是多面體P的面數,E是多面體P的棱的條數,X(P)是多面體P的歐拉示性數。如果P可以同胚於一個球面(可以通俗地理解為能...
歐拉類(Euler class)是實向量叢底空間的一個上同調類。定向實n維向量叢ξ的歐拉類是上同調類e(ξ)∈Hn(B;Z),在標準同構 π*:Hn(B;Z)→Hn(E;Z)下,它...
十八世紀瑞士數學家和物理學家倫哈特·歐拉(公元1707~公元1783)始終是世界最傑出的科學家之一。他的全部創造在整個物理學和許多工程領域裡都有著廣泛的套用。...
自然指數e,為自然對數的底數,有時亦稱之為歐拉數(Euler's Number),是一個無限不循環小數,其值約為:2.718281828459045235361。...
在模擬流體實驗時,最經常用到的三個準則數為雷諾數Re ,弗勞德數Fr 和歐拉數Eu 。雷諾數Re:主要受水流阻力即粘滯力作用的流體流動,凡是有壓流動,重力不影響流速...
