基本介紹
- 中文名:歐幾里德公理系統
- 外文名:Euolid axiomatic system
- 所屬學科:數學
- 提出時間:公元前3世紀
- 簡介:形式公理系統的前身
- 相關概念:公理系統
基本介紹
相關介紹
套用舉例
 圖1
圖1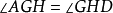

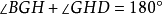
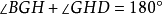
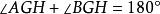
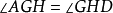
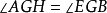


 圖1
圖1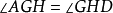

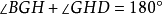
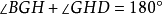
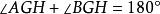
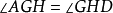
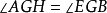

歐幾里德幾何公理系統是早期數學中最有影響的公理系統,大約提出於公元前3世紀。歐幾里德的公理系統E的結構是形式公理系統的前身,展示了數學知識之間的邏輯關係(作為...
幾何公理系統(geometric axiom system)一般指歐幾里得-希爾伯特幾何公理系統。歐幾里得的《幾何原本》是兩千多年間被公認為用嚴格的邏輯結構來敘述的科學典範,但用現代...
在《原本》里,歐幾里德系統地總結了古代勞動人民和學者們在實踐和思考中獲得的幾何知識,歐幾里德把人們公認的一些事實列成定義和公理,以形式邏輯的方法,用這些定義...
初始概念和公理是公理系統的出發點 [3] 。公理系統相應地區分為古典公理系統、現代公理系統或稱形式公理系統。最有代表性的古典公理系統是古希臘數學家歐幾里得在《...
古希臘數學家歐幾里德把人們公認的一些幾何知識作為定義和公理(公設),在此基礎上研究圖形的性質,推導出一系列定理,組成演繹體系,寫出《幾何原本》,形成了歐氏幾何...
幾何公理體系的基本問題包括公理體系的相容性、獨立性和完備性。是D.希爾伯特在《幾何基礎》一書中為完善歐幾里得幾何公理系統、各公理組間的邏輯關係而提出的。...
(3)規則是語法化的,它是符號生成轉換規則;公理的推導允許是非語法化的,即它的轉換不必遵循語法規則,只是基於內容的轉換一一如歐幾里德公理系統中的公理,它們是與...
它開創了古典數論的研究,在一系列公理、定義、公設的基礎上,創立了歐幾里得幾何學體系,成為用公理化方法建立起來的數學演繹體系的最早典範。...
非歐幾里得幾何是指不同於歐幾里得幾何學的幾何體系,簡稱為非歐幾何,一般是指羅巴切夫斯基幾何(雙曲幾何)和黎曼的橢圓幾何。它們與歐氏幾何最主要的區別在於公理體系中...
《歐幾里得幾何原本》是2003年6月1日陝西科學技術出版社出版的圖書。書中提出的幾乎所有的定理在歐幾里德之前就已經為人知曉,使用的許多證明亦是如此。...
它開創了古典數論的研究,在一系列公理、定義、公設的基礎上,創立了歐幾里得幾何學體系,成為用公理化方法建立起來的數學演繹體系的最早典範。...
羅巴切夫斯基幾何,也稱雙曲幾何,波利亞-羅巴切夫斯基幾何或羅氏幾何,是一種獨立於歐幾里得幾何的一種幾何公理系統。雙曲幾何的公理系統和歐氏幾何的公理系統不同之處...
第一個在歐幾里得幾何系統中構造出羅巴切夫斯基幾何公理系統模型的是法國數學家龐加萊(Poincaré,(J.-)H.),由於該模型與非歐幾何的相容性問題以及如何解決第五公設...
希爾伯特的《幾何基礎》把幾何學引進了一個更抽象的公理化系統,把幾何重新定義,不但把傳統的歐幾里得的《幾何原本》改良,更把幾何學從一種具體的特定模型上升為抽象...
歐幾里得《幾何原本》中套用的“阿基米德公理”成為近代幾何度量理論的基本公理之一...歐式幾何的傳統描述是一個公理系統,通過有限的公理來證明所有的“真命題”。歐式...
《幾何原本》開篇的第一個定理 歐幾里得幾何的傳統描述是一個公理系統,通過有限的公理來證明所有的“真命題”。歐幾里得平面幾何的五條公理(公設)是:...
它開創了古典數論的研究,在一系列公理、定義、公設的基礎上,創立了歐幾里得幾何學體系,成為用公理化方法建立起來的數學演繹體系的最早典範。...
拉斯學派和雅典學派的希波克拉底、柏拉圖、歐多克索斯等人的工作,使希臘亞歷山大學派的創始人歐幾里得在公元前約300年完成《幾何原本》,為幾何學系統化和公理化奠定了...
幾何度量是在D.希爾伯特建立的歐幾里得幾何的公理體系(見歐幾里得幾何學)的基礎上,線段度量的理論安排在連續公理之後,是以結合公理、順序公理、契約公理、連續公理等四...
立體幾何是建立在歐幾里得公理體系基礎上的三維空間幾何學,故又稱為三維歐幾里得幾何學,簡稱三維歐氏幾何。立體幾何是研究空間圖形的大小、形狀和相互位置關係等幾何性質...
