模糊線性規劃(fuzzy linear programming)是經典線性規劃的一種推廣,它是將線性約束的邊界模糊化,從而使人們能在較寬鬆的條件下求得最佳化的條件與最佳化的極值。
基本介紹
- 中文名:模糊線性規劃
- 外文名:fuzzy linear programming
- 所屬學科:數學(模糊數學)
- 簡介:經典線性規劃的一種推廣
基本介紹
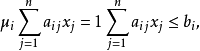
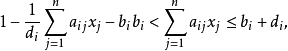
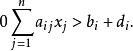
模糊線性規劃的模型
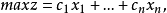
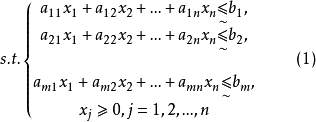
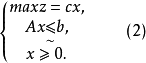
模糊線性規劃的求解
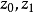
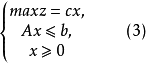
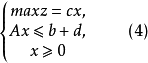
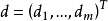
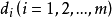
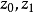
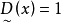
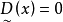
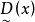
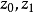
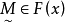
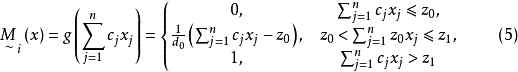
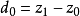
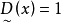
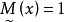
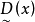
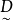
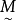
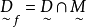
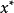
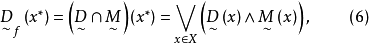
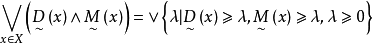
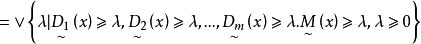
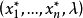
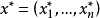
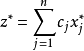
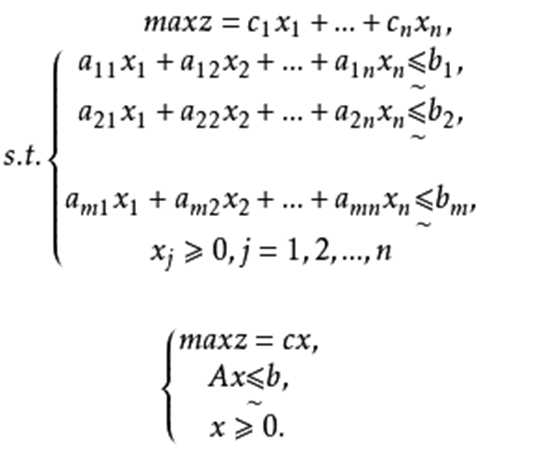
模糊線性規劃(fuzzy linear programming)是經典線性規劃的一種推廣,它是將線性約束的邊界模糊化,從而使人們能在較寬鬆的條件下求得最佳化的條件與最佳化的極值。
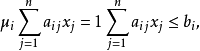
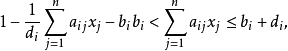
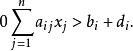
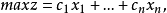
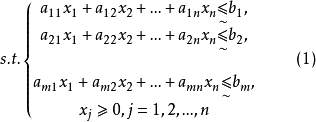
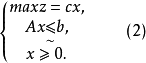
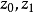
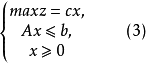
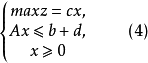
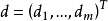
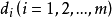
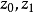
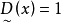
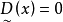
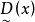
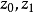
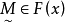
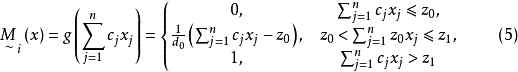
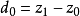
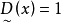
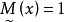
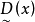
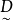
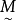
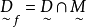
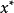
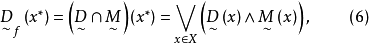
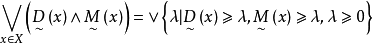
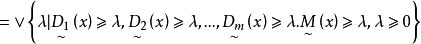
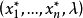
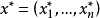
模糊線性規劃(fuzzy linear programming)是經典線性規劃的一種推廣,它是將線性約束的邊界模糊化,從而使人們能在較寬鬆的條件下求得最佳化的條件與最佳化的極值。...
第五章層次分析法介紹了模糊層次分析的建模方法與套用。第六章在普通線性規劃的基礎上,引入模糊線性規劃、多目標規劃的模糊最優解以及模糊線性規劃在經濟中的套用...
目標函式模糊化的一種途徑是以模糊數作為目標函式值,通過模糊數的分析、運算來尋求條件極值。約束條件的模糊化是將約束定義成模糊集合。在線性規劃中這樣的推廣導致...
作品信息基於模糊線性規劃和熵值法的虛擬企業任務分解風險評價研究1 作者: 王能 論文題名: 英文題名:Risk Evaluation of Task Decomposition of Virtual Enterprise ...
再到模糊隸屬函式和模糊關係,以及模糊問題向清晰問題的轉化; 其次介紹了模糊聚類、模式識別、模糊擴張原理、模糊推理、模糊控制、模糊決策、模糊線性規劃等原理和方法...
模糊關係、模糊相似性、模糊綜合評判、模糊邏輯、模糊推理、模糊控制系統、模糊模式識別、模糊專家系統、模糊神經網路、模糊遺傳算法、模糊線性規劃、模糊決策和直覺模糊...
內容簡介本書是工業與信息化部"十二五”規劃教材。全書包含基本理論部分和套用方法部分兩部分內容。其中,基本理論部分主要講述了模糊集合及其運算、模糊關係與模糊關係...
§6.4模糊層次分析法 習題六 第七章 模糊規劃 §7.1對稱的模糊規劃 §7.2不對稱的模糊規劃 §7.3模糊線性規劃 習題七 第八章 多目標決策的其他方法 §8.1...
基本理論涉及模糊集的基本概念、模糊集的基本定理、模糊關係和模糊矩陣、模糊圖等。建模方法包括模糊聚類分析,模糊模型識別,模糊決策,模糊線性規劃,模糊推理與控制等。...
本書講述模糊數學方法及其套用,主要內容包括:模糊集合及其運算、模糊統計方法、模糊聚類分析、模糊模型識別、模糊決策、模糊線性規劃等以及它們在科學技術與經濟管理中的...
內容包含格與模糊格、模糊集的基本理論、L型模糊集、模糊關係、模糊邏輯、模糊推理、模糊控制、模糊決策、模糊線性規劃以及模糊信息系統與知識獲取等,每章的後面都...
⒕基於規則和模糊線性規劃表示的專家系統研究. 《高技術通訊》,2004,14⑺:1- 4⒖基於劃分策略和填充曲線的抖動模式研究. 《計算機輔助設計與圖形學學報》,2001,...
(12) 模糊線性規劃在轉爐合金模型中的套用,江蘇大學學報(自然科學版)2002.1,(排名2/3)(13) 超媒體簡報系統的設計和實現,江蘇理工大學學報(自然科學版)2001.7...
模糊庫存、模糊線性規劃、模糊統籌理論等);2、複雜系統中的模糊結構元分析技術(包括:基於結構元理論的模糊幾何學、模糊線性系統以及模糊微分方程的研究);3模糊結構元...
《巨觀經濟系統中的保險總準備金適度規模研究》、《模糊線性規劃在企業管理中的套用》、《通識教育中自然科學課程建設之ABC》等數拾篇論文分別在《金融研究》、《...
