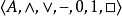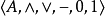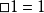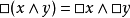模態代數

簡介

在代數和邏輯中，模態代數是代數結構

使得

是在A上的一元運算，對於所有A中的x,y滿足

和

。

模態代數提供了命題模態邏輯的模型，以和布爾代數是經典邏輯的模型相同的方式。特別是，所有模態代數的簇是在抽象代數邏輯意義下的模態邏輯K的等價代數語義，並且它的子簇們的格對偶同構於正規模態邏輯的格。

Stone布爾代數表示定理可以推廣為Jónsson–Tarski對偶性，它確保了每個模態代數可以表示為在模態一般框架內可容納的集合們的代數。

在抽象代數中，布爾代數(英語：Boolean algebra)是捕獲了集合運算和邏輯運算二者的根本性質的一個代數結構（就是說一組元素和服從定義的公理的在這些元素上運算）。特別是，它處理集合運算交集、並集、補集；和邏輯運算與、或、非。

模態邏輯，或者叫（不很常見）內涵邏輯，是處理用模態如“可能”、“或許”、“可以”、“一定”、“必然”等限定的句子的邏輯。模態邏輯可以用語義的“內涵性”來描述其特徵：複雜公式的真值不能由子公式的真值來決定的。允許這種決定性的邏輯是“外延性的”，經典邏輯就是外延性的例子。

在抽象代數中，內部代數是採用了集合的拓撲內部概念的特定類型的代數結構。內部代數之對於拓撲和模態邏輯S4如同布爾代數之對於集合論和普通命題邏輯。內部代數形成了模態代數的一個簇。