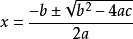
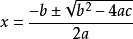
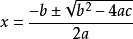
根式解(radical solution)方程的重要概念之一是一個代數方程的解,如果可以由這個方程的係數經過有限次加、減、乘、除以及開整數次方等運算表示出來,就稱為這個方程...
方程根式解(solvability of equation by radi-cats)一個著名的古典數學問題.域F上次數>1的多項式f<x),若方程f(x)=0。的每個根都可由f <x>的係數經過加、...
《代數方程的根式解及伽羅瓦理論》是2011年哈爾濱工業大學出版社出版的圖書,作者是謝彥麟。本書適合大學、中學師生及數學愛好者閱讀。...
許多方程不存在解析解,或是沒有簡單形式的解析解,例如五次方程以及更高次的代數方程,不存在根式解(用有限次的四則運算及根號組合而成的解析解),這是由數學家...
數學中的方程求解是指找出哪些值(可能是數、函式、集合)可以使一個方程成立,或是指出這様的解不存在。方程是兩個用等號相連的數學表示式,表示式中有一個或多個...
根式擴域(radical extension)是一種有限擴域,是與代數方程的根式解相關的擴域。域F的一個擴域K,若存在一個子域鏈:使得其中F=F (a),且必EF不能被F的特徵...
“阿貝爾不可能性定理”—— 一般五次方程無根式求解,開啟了代數史上的一個偉大的新紀元,是人類思想史上的一個重大事件,“她”深刻而優美,但卻由於坊間的書籍與...
換句話說,只有三次和四次的高次方程可用根式求解。 對於5次以上的方程,一般的公式和求根定理已經不能實現,必須尋求新的方法。在數值方法中,一般的求根算法只能求...
求一元五次方程的根式解曾困擾數學家三百餘年,阿貝爾和伽羅瓦的工作證明了一般一元五次方程沒有根式解。1930 年華羅庚《蘇家駒之代數的五次方程式解法不能 成立之...
五次方程是一種最高次數為五次的多項式方程。尋找五次方程的解一直是個重要的數學問題。一次方程和二次方程很早就找到了公式解,經過數學家們的努力,後來三次方程...
伽羅瓦理論是用群論的方法來研究代數方程的解的理論。在19世紀末以前,解方程一直是代數學的中心問題。早在古巴比倫時代,人們就會解二次方程。在許多情況下,求解的...
兩種公式法都可以解標準型的一元三次方程。用卡爾丹公式解題方便,相比之下,盛金...公之於世,加速了一元三次方程求根公式的普及和人類探索一元n次方程根式解法的...
五次方程是未知項總次數最高為5的整式方程。一般的五次方程沒有統一的公式解存在。...... 1830年:法國數學天才伽羅瓦徹底解決了5次方程何時可以根式解的問題。可是...
克羅內克定理(Kronecker theorem)關於代 數方程可根式解的命題...... 克羅內克定理(Kronecker theorem)關於代 數方程可根式解的命題.定理解釋設n為奇素數,f(二)是...
研究一元n次方程的根,包括根的存在、根式解、根的界和根的個數等,曾經是代數學的中心問題,一元n次方程的係數和有理常數以及對這些數進行加、減、乘、除和開...
這是一元十次方程的完整版求根公式,雖說有些十次方程能因式分解求根,但卻不能用通解公式表達。根據阿貝爾定理,大於四次的方程沒有根式通解;所以天珩公式也僅對...
魯菲尼-阿貝爾定理(theorem of Ruffini-Abel)最早出現的代數方程能否用根式解的判別定理。...
存在公式可以測試這兩種情況,並在方程有解的時候求出用根式表示的根。一般的六次方程可以通過Kampé de Fériet函式(超幾何函式的一個雙變數擴展版)求解。一類特殊...
次根;標準四次方程的對應多項式可以分解成兩個二次式的乘積,其係數在求出對應三次方程的一個根後也可用公式求出;五次及五次以上的代數方程一般不能用根式求解。...
