魯菲尼-阿貝爾定理(theorem of Ruffini-Abel)最早出現的代數方程能否用根式解的判別定理。
.設F是特徵為零的域,t
1,t2...,tn,是F上不相關未定元,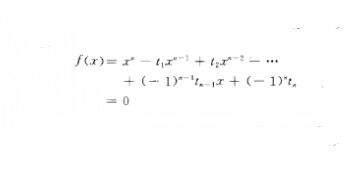
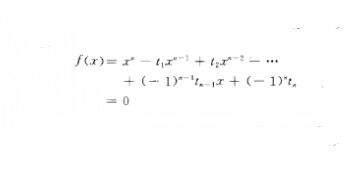
稱為F上的n次一般方程.若f.(二)是F上可分不可約多項式,則f(x)在F上的伽羅瓦群與,,次對稱群S。同構.魯菲尼(Ruffini,P.)和阿貝爾(Abel, N.H.)證明:當n}4時,f<二)不能用根式解.這個結論通常稱為魯菲尼一阿貝爾定理.事實上,當n=2,3,4時,凡是可解群;當n>4時,Sn不是可解群.
魯菲尼-阿貝爾定理(theorem of Ruffini-Abel)最早出現的代數方程能否用根式解的判別定理。
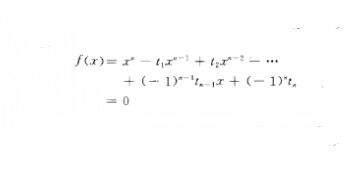
阿貝爾—魯菲尼定理指出,五次及更高次的代數方程沒有一般的代數解法,即這樣的方程不能由方程的係數經有限次四則運算和開方運算求根。...
魯菲尼-阿貝爾定理(theorem of Ruffini-Abel)最早出現的代數方程能否用根式解的判別定理。...
主要成就 證明了五次及五次以上的方程不能用公式求解(魯菲尼-阿貝爾定理) 代表作品 論文《一元五次方程沒有代數一般解》(1824年) 目錄...
但阿貝爾在立下一定要證出的誓言後,便日夜不停的用自己所學知識試圖證明。皇天不負有心人,阿爾貝證明出了此次 方程有解並命名為魯菲尼定理。若阿爾貝當時只想等...
