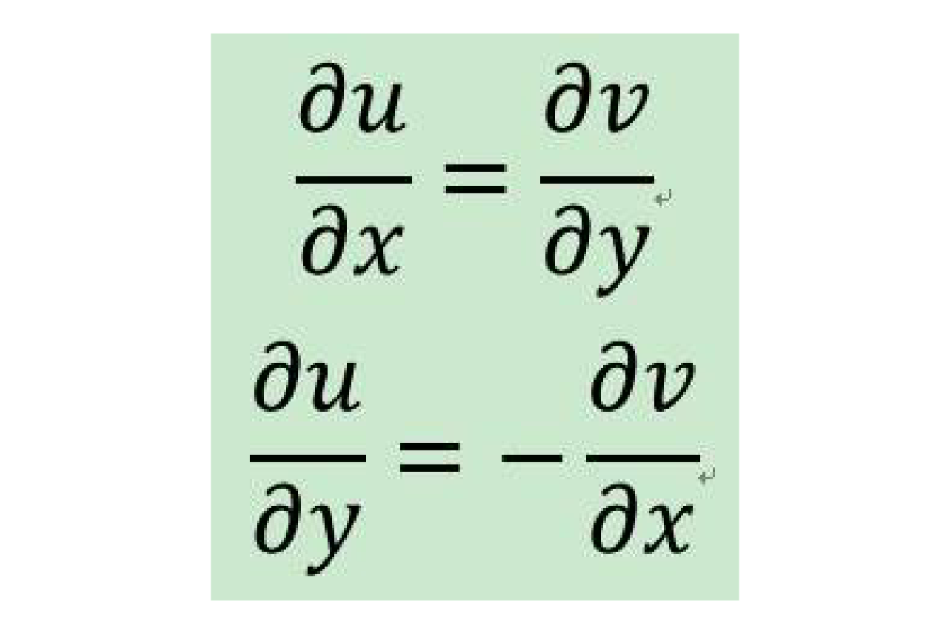柯西-黎曼方程

柯西-黎曼微分方程是提供了可微函式在開集中為全純函式的充要條件的兩個偏微分方程，以柯西和黎曼得名。這個方程組最初出現在達朗貝爾的著作中。後來歐拉將此方程組和解析函式聯繫起來。 然後柯西採用這些方程來構建他的函式理論。黎曼關於此函式理論的論文於1851年問世。

基本介紹

• 中文名：柯西-黎曼方程
• 外文名：Cauchy-Riemann Equations
• 屬性：偏微分方程
• 學科：數理
• 簡稱：C-R方程
• 發明者：柯西
• 發展者：黎曼

研究歷史

複分析中的柯西-黎曼微分方程是提供了可微函式在開集中全純函式的充要條件的兩個偏微分方程，以柯西和黎曼得名。這個方程組最初出現在達朗貝爾的著作中(d'Alembert 1752)。後來歐拉將此方程組和解析函式聯繫起來(Euler 1777)。 然後柯西(Cauchy 1814)採用這些方程來構建他的函式理論。黎曼關於此函式理論的論文(Riemann 1851)於1851年問世。

方程

在一對實值函式 和 上的柯西-黎曼方程組包括兩個方程：

(1)

(2)

柯西-黎曼方程是函式在一點可微的必要條件。

設函式 在區域D內有定義，則它在D內解析的充分必要條件是：

1） 與 在D內處處可微；

2） 與 在D內處處滿足一階偏微分方程組 ， 。

證明過程

設函式 定義在區域D內，並在D內一點 可導（或可微），於是

式中， 滿足 .

其中

則

代入式

並比較實部和虛部得

由於 ，

因此 及 在點 可微，並且成立

方程

，

稱為柯西-黎曼（Cauchy-Riemann）方程，簡稱C-R方程。

這就得到了 在點z可導的必要條件。實際上，這個條件也是充分的，以下證明充分性。

設 ， 在點 可微，則有

於是由C-R方程得

其中，

由於 ，

因此

即函式 在 可導。

由以上討論可知，當定理的條件滿足時， 在點z的導數為：