表示相空間相鄰軌跡的平均指數發散率的數值特徵。又稱李雅普諾夫特徵指數,是用於識別混沌運動若干數值的特徵之一。
基本介紹
- 中文名:李雅普諾夫指數
- 外文名:Lyapunov exponent
- 性質:科學
- 類別:數學、力學

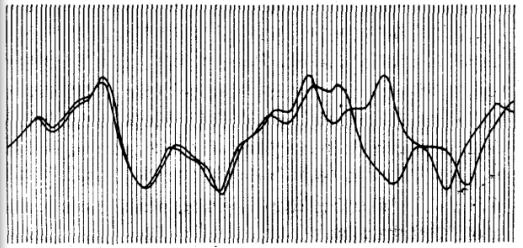 此圖取自洛倫茲1961年的列印結果
此圖取自洛倫茲1961年的列印結果
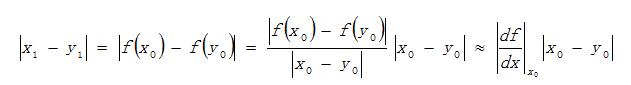

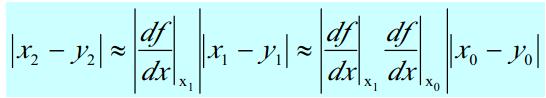





套用
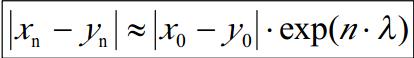
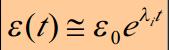

表示相空間相鄰軌跡的平均指數發散率的數值特徵。又稱李雅普諾夫特徵指數,是用於識別混沌運動若干數值的特徵之一。

 此圖取自洛倫茲1961年的列印結果
此圖取自洛倫茲1961年的列印結果
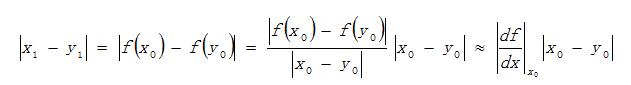

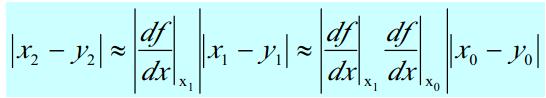





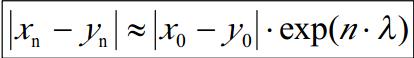
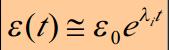

表示相空間相鄰軌跡的平均指數發散率的數值特徵。又稱李雅普諾夫特徵指數,是用於識別混沌運動若干數值的特徵之一。...
李雅普諾夫指數 外文名 Lyapunov exponents 基本特點 系統對初始值的極端敏感性 衡量 系統動力學特性 性質 一個重要定量指標 目錄...
在自動控制領域中,李雅普諾夫穩定性(英語:Lyapunov stability,或李亞普諾夫穩定性)可用來描述一個動力系統的穩定性。如果此動力系統任何初始條件在平衡態附近的軌跡均...
李雅普諾夫是俄國著名的數學家、力學家。1857年6月6日生於雅羅斯拉夫爾,1918年11月3日卒於敖德薩。19世紀以前,俄國的數學是相當落後的,直到切比雪夫創立了聖彼得堡...
書中還介紹了相關非線性動力學的基礎知識,如混沌、分形、準周期、共振、李雅普諾夫指數等,以及這些觀念在分子高激發振動動力學研究中的套用。...
7.6李雅普諾夫指數7.7混沌吸引子的檢驗7.8套用7.9理論與證明練習第二部分疊函式第8章動力系統中的疊函式8.1一維映射8.2多變數函式第9章一維映射的周期點...
▪ 小波變換 ▪ 洛倫茨曲線 ▪ 數據包絡分析 ▪ 李雅普諾夫指數 ▪ 曼-肯德爾算法 ▪ 可計算一般均衡 ▪ 環境可計算一般均衡 ▪ 空間可計算一般...
2.2.3 邏輯斯蒂映射的李雅普諾夫指數計算2.3 狀態演化的數學模型2.3.1 帳篷映射與鋸齒映射2.3.2 巴克爾變換映射2.3.3 斯梅爾馬蹄映射...
非線性混沌系統正李雅普諾夫指數 在發現混沌之前,人們認為確定系統存在三種運動狀態:定態、準周期態和周期態。混沌態的發現改變了人們的這一固有看法,混沌系統具有...
4.4 進一步閱讀:李雅普諾夫指數習題4.1參考文獻常微分方程與動力系統概論前言 編輯 常微分方程是研究動力系統的重要基礎。目前,關於常微分方程和動力系統這兩門學科的...
混沌系統控制與控制論中的經典控制問題不同,混沌從總體上迄今尚無統一的共同的理論框架,但是混沌控制的機制上有一個共同點,就是變原來正的李雅普諾夫指數為負值,...
11隨移李雅普諾夫指數 12空間倍周期分岔行為 第5章 全程耦合映象 13模型的時空行為和分類 14有序行為中的開關現象 15無序行為中的漲落問題 第6章 交叉耦合映象...
並通過對資本市場時間序列的相空間重構,計算了資本市場的分形維和李雅普諾夫指數,從而完成了對資本市場的動力學分析。有效市場假說作為金融經濟學的基礎理論之一,自...
-為計算李雅普諾夫指數增加Range運算-增加GIF編碼器VERSION 4.55 Aug 2000為CVODE增加邊界版本VERSION 4.3 January 2000a. 修復部分bug, 處理參數增加到400個...
5.8 奇怪吸引子與李雅普諾夫指數5.9 混沌時間序列的相容間重構5.10 混沌的控制與同步5.11 混沌的套用領域5.12 混沌學的哲學思想第6章 分形複雜性科學篇...
3.5李雅普諾夫特徵指數 4非線性蛛網模型 4.1蛛網模型 4.2幼稚預期 4.3理性預期 4.4複雜市場中的幼稚預期 4.5適應性預期 4.6線性回顧預期 4.7行為理性的線性預測規則 ...
2.5 李雅普諾夫指數與混沌2.6 譜分析2.7 不同吸引子的描述2.8 從時間序列重構吸引子練習題第3章 離散動力系統3.1 引例3.2 一維映射...
混沌狀態可以藉助於李雅普諾夫指數來描述。 對於一個自由度N ≥ 2的哈密頓力學系統, 其哈密頓函式為:H(p,q) = + U(q) (1)則系統的運動由哈密頓正則方程...
