基本介紹
簡介,按方程方法,決定論,系統演化,可計算性,性質,精度,行為,定律,缺點,預言,動力學,含義,
簡介
【相空間解釋】
相空間(phase space)
作為一個巨大維數的空間，它上面的每個點代表我們考慮的系統全部可能的態。
按方程方法
我們如何按照相空間來摹想哈密頓方程呢？首先，我們要記住相空間的單獨的點Q實際代表什麼。它代表所有位置坐標x1，x2，…和所有動量坐標p1，p2，…的一種特別的值。也就是說，Q表示我們整個物理系統，指明組成它的所有單獨粒子的特定的運動狀態。當我們知道它們現在的值時，哈密頓方程告訴我們所有這些坐標的變化率是多少，亦即它控制所有單獨的粒子如何移動。
翻譯成相空間語言，該方程告訴我們，如果給定單獨的點Q在相空間的現在位置的話，它將會如何移動。為了描述我們整個系統隨時間的變化，我們在相空間的每一點都有一個小箭頭，更準確地講，一個矢量，它告訴我們Q移動的方式。
決定論
我們看看如何按照相空間來解釋物理的決定論。對於時間t=0的初始數據，我們有了一組指明所有位置和動量坐標的特定值；也就是說，我們在相空間特別選定了一點Q。為了找出此系統隨時間的變化，我們就跟著箭頭走好了，這樣，不管一個系統如何複雜，該系統隨時間的整個演化在相空間中僅僅被描述成一點沿著它所遭遇到的特定的箭頭移動。
“長”的箭頭表明Q移動得快，而“短”的箭頭表明Q的運動停滯。只要看看Q以這種方式隨著箭頭在時間t移動到何處，即能知道我們物理系統在該時刻的狀態。很清楚，這是一個決定性的過程。Q移動的方式由哈密頓矢量場所完全決定。
系統演化
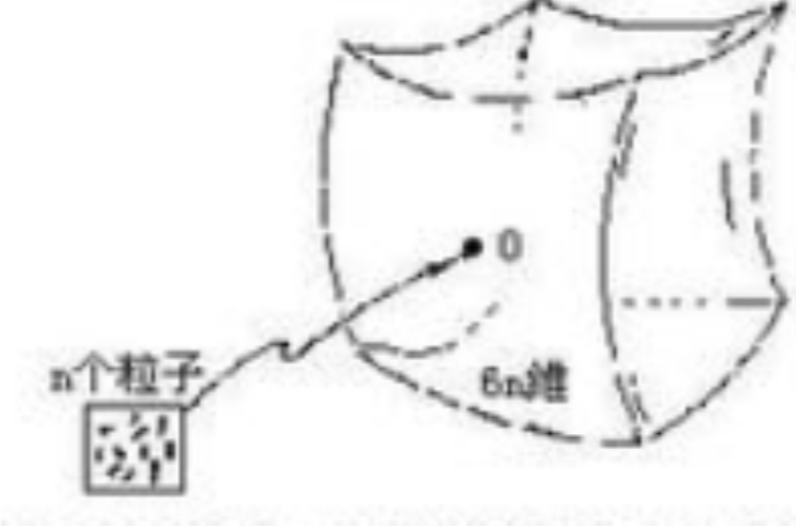
哈密頓方程的形式允許我們以一種非常強而有力的一般方式去“摹想”經典系統的演化。想像一個多維“空間”，每一維對應於一個坐標x1,x2,…p1,p2,…（數學空間的維數，通常比3大得多。）此空間稱之為相空間。對於n個無約束的粒子。相空間就有6n維（每個粒子有三個位置坐標和三個動量坐標）。讀者或許會擔心，甚至只要有一個單獨粒子，其維數就是他或她通常所能摹想的二倍！不必為此沮喪！儘管六維的確是能比明了畫出的更多的維數，但是即使我們真的把它畫出也無太多用處。僅僅就一滿屋子的氣體，其相空間的維數大約就有10,000,000,000,000,000,000,000,000,000
可計算性
另一方面，由於類似於我在討論有關撞球世界時簡要提出的理由，對我來說，這似乎不完全是相關的問題。為了使一個相空間的點是不可計算的斷言有意義，它要求無限精確的坐標??亦即它的所有小數位！（一個由有限小數描述的數總是可以計算的。）一個數的小數展開的有限段不能告訴我們任何關於這個數整個展開的可計算性。但是，所有物理測量的精度都是有限的，只能給出有限位小數點的信息。在進行物理測量時，這是否使“可計算數”的整個概念化成泡影？”
的確，一個以任何有用的方式利用某些物理定律中（假想的）不可計算因素的儀器不應依賴於無限精確的測量。也許我在這裡有些過分苛刻了。假定我們有一台物理儀器，為了已知的理論原因，模擬某種有趣的非算法的數學過程。如果此儀器的行為總可以被精密地確定的話，則它的行為就會給一系列數學上有趣的沒有算法的是非問題以正確答案。任何給定的算法都會到某個階段失效。而在那個階段，該儀器會告訴我們某些新的東西。該儀器也許的確能把某些物理常數測量到越來越高的精度。而為了研究一系列越來越深入的問題，這是需要的。然而，在該儀器的有限的精度階段，至少直到我們對這系列問題找到一個改善的算法之前，我們得到某些新的東西。然而，為了得到某些使用改善了的算法也不能告訴我們的東西，就必須乞求更高的精度。
性質
精度
儘管如此，不斷提高物理常數的精度看來仍是一個棘手和不盡人意的信息編碼的方法。以一種分立（或“數字”）形式得到信息則好得多。如果考察越來越多的分立單元，也可重複考察分立單元的固定集合，使得所需的無限的信息散開在越來越長的時間間隔里，因此能夠回答越來越深入的問題。（我們可以將這些分立單元想像成由許多部分組成，每一部分有“開”和“關”兩種狀態，正如在第二章描述的圖靈機的0和1狀態一樣。）為此看來我們需要某種儀器，它能夠（可區別地）接納分立態，並在系統按照動力學定律演化後，又能再次接納一個分立態集合中的一個態。如果事情是這樣的話，則我們可以不必在任意高的精度上考察每一台儀器。
行為
那么，哈密頓系統的行為確實如此嗎？某種行為的穩定性是必須的，這樣才能清晰地確定我們的儀器實際上處於何種分立態。一旦它處於某狀態，我們就要它停在那裡（至少一段相當長的時間），並且不能從此狀態滑到另一狀態。不但如此，如果該系統不是很準確地到達這些狀態，我們不要讓這種不準確性累積起來；我們十分需要這種不準確性隨時間越變越小。我們現在構想的儀器必須由粒子（或其他子元件）所構成。需要以連續參數來描述粒子，而每一個可區別的“分立”態覆蓋連續參數的某個範圍。（例如，讓粒子停留在二個盒子中的一個便是一種表達分立雙態的方法。為了指明該粒子確實是在某一個盒子中，我們必須斷定其位置坐標在某個範圍之內。）用相空間的語言講，這表明我們的每一個“分立”的態必須對應於相空間的一個“區域”，同一區域的相空間點就對應於我們儀器的這些可選擇的同一態。
現在假定儀器在開始時的態對應於它的相空間中的某一個範圍R0。我們想像R0隨著時間沿著哈密頓矢量場被拖動，到時刻t該區域變成Rt。在畫圖時，我們同時想像對應於同一選擇的所有可能的態的時間演化。關於穩定性的問題（在我們感興趣的意義上講）是，當t增加時區域Rt是否仍然是定域性的，或者它是否會向相空間散開去。如果這樣的區域在時間推進時仍是定域性的，我們對此系統就有了穩定性的量度。在相空間中相互靠近的點（這樣它們對應於相互類似的系統的細緻的物理態）將繼續靠得很近，給定的態的不準確性不隨時間而放大。任何不正常的彌散都會導致系統行為的等效的非預測性。
定律
我們對於哈密頓系統可以一般地說什麼呢？相空間的區域究竟是否隨時間散開呢？似乎對於一個如此廣泛的問題，很少有什麼可說的。然而，人們發現了一個非常漂亮的定理，它要歸功於傑出的法國數學家約瑟夫·劉維爾（1809--1882）。該定律講，相空間中的任何區域的體積在任何哈密頓演化下必須保持常數。（當然，由於我們的相空間是高維的，所以“體積”必須是在相應高維意義上來說的。）這樣，每一個R1的體積必須和原先的R0的體積一樣。初看起來，這給了我們的穩定性問題以肯定的答案。在相空間體積的這層意義上，我們區域的尺度不能變大，好像我們的區域在相空間中不會散開似的。
然而，這是使人誤解的。我們在深思熟慮之後就會感到，很可能情況剛好與此相反！我想表示人們一般預料到的那種行為。我們可以將初始區域R0想像成一個小的、“合理的”，亦即較圓的而不是細長的形狀。這表明屬於R0的態在某種方面不必賦予不合情理的精確性。然而，隨著時間的發展，區域R1開始變形並拉長--初看起來有點像變形蟲，然後伸長到相空間中很遠的地方，並以非常複雜的方式糾纏得亂七八糟。體積的確是保持不變，但這個同樣小的體積會變得非常細，再發散到相空間的巨大區域中去。這和將一小滴墨水放到一大盆水中的情形有點類似。雖然墨水物質的實際體積不變，它最終被稀釋到整個容器的容積中去。區域Rt在相空間中的行為與此很類似。它可能不在全部相空間中散開（那是稱之為“愛哥狄克”的極端情況），但很可能散開到比原先大得極多的區域去。（可參閱戴維斯（1974）的進一步討論。）
缺點
麻煩在於保持體積並不意味就保持形狀：小區域會被變形，這種變形在大距離下被放大。由於在高維時存在區域可以散開去的多得多的“方向”，所以這問題比在低維下嚴重得多。事實上，劉維爾定理遠非“幫助”我們將區域Rt控制住，而是向我們提出了一個基本問題！若無劉維爾定理，我們可以摹想相空間中區域的毫無疑義的發散趨勢可由整個空間的縮小而補償。然而，這一個定律告訴我們這是不可能的，而我們必須面對這個驚人的含義——這個所有正常類型的經典動力學（哈密頓）系統的普適的特徵9！
預言
鑒於這種發散到整個相空間去的行為，我們會問，經典力學怎么可能作出預言？這的確是一個好問題。這種彌散所告訴我們的是，不管我們多么精確地（在某一合理的極限內）知道系統的初始態，其不確定性將隨著時間而不斷增大，而我們原始的信息幾乎會變得毫無用處。在這個意義上講，經典力學基本上是不可預言的。（回想前面考慮過的“混沌”概念）
動力學
那么，何以迄今為止牛頓動力學顯得如此之成功呢？在天體力學中（亦即在引力作用下的天體）其原因在於，第一，有關的凝聚的物體數目相對很少（太陽、行星和月亮），這些物體的質量相差懸殊?這樣在估量近似值時，可以不必管質量更小物體的微擾效應，而處理更大的物體時，僅僅需要考慮它們相互作用的影響。第二，可以看到，適用於構成這些物體的個別粒子的動力學定律，也可以在這些物體本身上的水平上適用--這使得在非常好的近似下，太陽、行星和月亮實際上可以當作粒子來處理，我們不必去為構成天體的單獨粒子的運動的微小細節去擔憂。我們再次只要考慮“很少”的物體，其在相空間中的彌散不重要。
除了天體力學和投擲物行為（它其實是天體力學的一個特例）之外，只牽涉到小數目的粒子的簡單系統的研究，牛頓力學所用的主要方法是根本不管這些細節的“可決定性地預言的”方面。相反地，人們利用一般的牛頓理論做模型，從這些模型可以推導出整體行為。某些諸如能量、動量和角動量守恆定律的準確推論的確在任何尺度下都有效。此外，存在可與制約單獨粒子的動力學規律相結合的統計性質，它能對有關的行為作總體預言。（參閱關於熱力學的討論；我們剛討論過的相空間彌散效應和熱力學第二定律有緊密的關係。我們只要相當仔細，便可利用這些觀念作預言。）牛頓本人所做的空氣聲速的計算（1個世紀後拉普拉斯進行了微小的修正）便是一個好例子。然而，經典動力學（牛頓~拉格朗日~哈密頓的演變）中忽略微小擾動的思維模式在近代物理學上實際上適用的機會非常稀少。
含義
相空間彌散效應還有一個驚人的含義。它告訴我們，經典力學不能真正地描述我們的世界！我說得有點過分了一些，但是並不太過分。經典力學可以很好地適用於流體--特別是氣體的行為，在很大的程度上適用於液體--此處人們只關心粒子系統的“平均”性質，但是在對固體作計算時就出了毛病，這裡要求知道更細節的組織結構。固體由億萬顆點狀的粒子所組成，由於相空間彌散其排列的有序性應不斷地降低，何以保持其形狀大致不變呢？正如我們已經知道的，量子力學在理解固體的實在結構時是不可或缺的。量子效應可多多少少防止相空間的彌散。
這也和製造“計算機器”的問題相關。相空間彌散是某種必須控制的東西。相空間中對應於一個電腦的“分立”態的區域（例如前述的R0）不應允許其過度彌散開來。我們記得，甚至弗列得欽--托弗里“撞球電腦”需要某種外圍的固體牆才能工作。包括許多粒子的物體的“剛性”正是需要量子力學起作用的某種東西。
以相空間重構理論為基礎，採用Takens定理重構語音信號相空間並提取相似序列重複度(RPT)特徵參數，利用清濁音RPT參數的差異，提出並實現了一種採用BP神經網路進行非線性清濁音判決的方法，得到了明顯優於傳統算法的結果，本文方法為語音特徵提取和識別研究提供了新的途徑。
