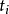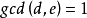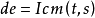令K是域F的一個擴域.一個元素a如果它生成擴域K/F,即K=F(a),則稱該元索為該擴域的本原元。本原元很有用,因為如果a在F上的既約多項式已知,那么在F(a)上的運算會很容易進行。
基本介紹
- 中文名:本原元
- 外文名:primitive element
- 所屬學科:數學
- 意義:有限域乘法特性的主要表現
定義,主要性質,本原元定理,定理內容,本原元定理的證明,求本原元的高斯算法,
定義
本原元是有限域乘法特性的主要表現。
與循環群類似,記域元素 的冪為
的冪為


定義1 非零域元素 的階
的階 是其冪為單位元的最小冪指數,即
是其冪為單位元的最小冪指數,即


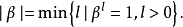
定義2 稱具有最大階的域元素為本原元,即對本原元 ,有
,有


主要性質
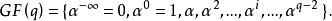
(2)(本原元的計數定理)GF(q)中有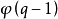 個本原元,這裡
個本原元,這裡 為歐拉函式,其值為小於n且與n互素的非零正整數的個數,即
為歐拉函式,其值為小於n且與n互素的非零正整數的個數,即
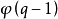


因為由域的定義,有限域的非零元素集合對域乘法形成一個有限交換群,而有限交換群一定是循環群,所以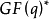 中存在生成元
中存在生成元 ,使得
,使得 ,從而循環群
,從而循環群 中生成元的個數
中生成元的個數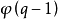 就是
就是 中本原元的個數。
中本原元的個數。
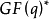



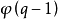

本原元定理
定理內容
特徵為零的域F的任何有限擴域K包含本原元。
註:這個命題當F是有限域的時候也是成立的,只是證明不同。對於特徵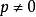 的無限域,定理需要更多的假設條件,因為我們不研究這樣的域,因此不考慮這種情況。
的無限域,定理需要更多的假設條件,因為我們不研究這樣的域,因此不考慮這種情況。
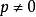
本原元定理的證明
由於擴域K/F是有限擴域,故K由有限集合生成,例如K作為F-向量空間的一組基就在F上生成K,設 ,我們對於k套用歸納法,當
,我們對於k套用歸納法,當 ,無需證明,假設k>l,歸納假設定理對於域
,無需證明,假設k>l,歸納假設定理對於域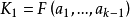 成立,該域
成立,該域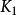 由前k一1個元素
由前k一1個元素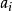 生成,故我們可以假設
生成,故我們可以假設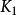 由單個元素
由單個元素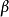 生成,所以K由兩個元素
生成,所以K由兩個元素 和
和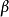 生成,定理的證明於是簡化為K由兩個元素生成的情形,下面的引理解決這種情形。
生成,定理的證明於是簡化為K由兩個元素生成的情形,下面的引理解決這種情形。


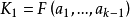
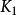
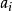
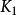
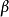

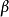
引理 令F是特徵為零的域,令K是由兩個元素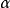 和
和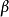 在F上生成的擴域,除去F中有限多個c之外,
在F上生成的擴域,除去F中有限多個c之外,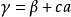 是K在F上的本原元。
是K在F上的本原元。
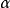
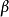
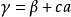
求本原元的高斯算法
在比較大的域中,需要一個系統的方法來尋找本原元,下面給出一個尋找任意有限域中本原元的高斯算法。
在此算法中我們需要依次處理域元素序列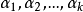 ,其中
,其中 ,
, ,實際上,對於
,實際上,對於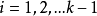 ,有
,有
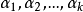


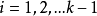

高斯算法:
第一步:設i=1,取域F中的任意一個非零元 ,且記
,且記 ;
;


第二步:若 ,則算法停止,
,則算法停止, 即為所尋找的本原元,否則轉第三步;
即為所尋找的本原元,否則轉第三步;


第三步:在域F中選一個非 的冪次的非零元
的冪次的非零元 ,設
,設 ,若s=q一1,則令
,若s=q一1,則令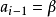 ,算法停止;否則轉第四步。
,算法停止;否則轉第四步。



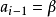
第四步:尋找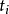 的一個因子d,s的一個因子e,使得
的一個因子d,s的一個因子e,使得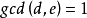 且
且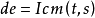 ,設
,設