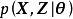最大期望算法(Expectation-Maximization algorithm, EM),或Dempster-Laird-Rubin算法,是一類通過疊代進行極大似然估計(Maximum Likelihood Estimation, MLE)的最佳化算法,通常作為牛頓疊代法(Newton-Raphson method)的替代用於對包含隱變數(latent variable)或缺失數據(incomplete-data)的機率模型進行參數估計。
EM算法的標準計算框架由E步(Expectation-step)和M步(Maximization step)交替組成,算法的收斂性可以確保疊代至少逼近局部極大值。EM算法是MM算法(Minorize-Maximization algorithm)的特例之一,有多個改進版本,包括使用了貝葉斯推斷的EM算法、EM梯度算法、廣義EM算法等。
由於疊代規則容易實現並可以靈活考慮隱變數,EM算法被廣泛套用於處理數據的缺測值,以及很多機器學習(machine learning)算法,包括高斯混合模型(Gaussian Mixture Model, GMM)和隱馬爾可夫模型(Hidden Markov Model, HMM)的參數估計。
基本介紹
- 中文名:最大期望算法
- 外文名:Expectation Maximization algorithm, EM
- 類型:最佳化算法
- 提出者:Arthur Dempster,Nan Laird,
- :Donald Rubin 等
- 提出時間:1977年
- 套用:數據分析,機器學習
歷史
理論

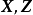








算法
標準算法






 EM的計算框架:對數似然(藍),E步(綠),M步(實心點)
EM的計算框架:對數似然(藍),E步(綠),M步(實心點)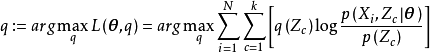



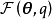




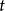
 E步:最佳化代理損失(左),原最佳化目標(右)
E步:最佳化代理損失(左),原最佳化目標(右)

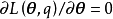

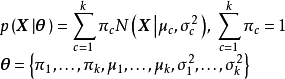
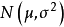













# 導入模組import numpy as npimport matplotlib.pyplot as pltfrom scipy.stats import multivariate_normal# 構建測試數據N = 200; pi1 = np.array([0.6, 0.3, 0.1])mu1 = np.array([[0,4], [-2,0], [3,-3]])sigma1 = np.array([[[3,0],[0,0.5]], [[1,0],[0,2]], [[.5,0],[0,.5]]])gen = [np.random.multivariate_normal(mu, sigma, int(pi*N)) for mu, sigma, pi in zip(mu1, sigma1, pi1)]X = np.concatenate(gen)# 初始化: mu, sigma, pi = 均值, 協方差矩陣, 混合係數theta = {}; param = {}theta['pi'] = [1/3, 1/3, 1/3] # 均勻初始化theta['mu'] = np.random.random((3, 2)) # 隨機初始化theta['sigma'] = np.array([np.eye(2)]*3) # 初始化為單位正定矩陣param['k'] = len(pi1); param['N'] = X.shape[0]; param['dim'] = X.shape[1]# 定義函式def GMM_component(X, theta, c): ''' 由聯合常態分配計算GMM的單個成員 ''' return theta['pi'][c]*multivariate_normal(theta['mu'][c], theta['sigma'][c, ...]).pdf(X)def E_step(theta, param): ''' E步:更新隱變數機率分布q(Z)。 ''' q = np.zeros((param['k'], param['N'])) for i in range(param['k']): q[i, :] = GMM_component(X, theta, i) q /= q.sum(axis=0) return qdef M_step(X, q, theta, param): ''' M步:使用q(Z)更新GMM參數。 ''' pi_temp = q.sum(axis=1); pi_temp /= param['N'] # 計算pi mu_temp = q.dot(X); mu_temp /= q.sum(axis=1)[:, None] # 計算mu sigma_temp = np.zeros((param['k'], param['dim'], param['dim'])) for i in range(param['k']): ys = X - mu_temp[i, :] sigma_temp[i] = np.sum(q[i, :, None, None]*np.matmul(ys[..., None], ys[:, None, :]), axis=0) sigma_temp /= np.sum(q, axis=1)[:, None, None] # 計算sigma theta['pi'] = pi_temp; theta['mu'] = mu_temp; theta['sigma'] = sigma_temp return thetadef likelihood(X, theta): ''' 計算GMM的對數似然。 ''' ll = 0 for i in range(param['k']): ll += GMM_component(X, theta, i) ll = np.log(ll).sum() return lldef EM_GMM(X, theta, param, eps=1e-5, max_iter=1000): ''' 高斯混合模型的EM算法求解 theta: GMM模型參數; param: 其它係數; eps: 計算精度; max_iter: 最大疊代次數 返回對數似然和參數theta,theta是包含pi、mu、sigma的Python字典 ''' for i in range(max_iter): ll_old = 0 # E-step q = E_step(theta, param) # M-step theta = M_step(X, q, theta, param) ll_new = likelihood(X, theta) if np.abs(ll_new - ll_old) < eps: break; else: ll_old = ll_new return ll_new, theta# EM算法求解GMM,最大疊代次數為1e5ll, theta2 = EM_GMM(X, theta, param, max_iter=10000)# 由theta計算聯合常態分配的機率密度L = 100; Xlim = [-6, 6]; Ylim = [-6, 6]XGrid, YGrid = np.meshgrid(np.linspace(Xlim[0], Xlim[1], L), np.linspace(Ylim[0], Ylim[1], L))Xout = np.vstack([XGrid.ravel(), YGrid.ravel()]).TMVN = np.zeros(L*L)for i in range(param['k']): MVN += GMM_component(Xout, theta, i)MVN = MVN.reshape((L, L))# 繪製結果plt.plot(X[:, 0], X[:, 1], 'x', c='gray', zorder=1)plt.contour(XGrid, YGrid, MVN, 5, colors=('k',), linewidths=(2,))改進算法










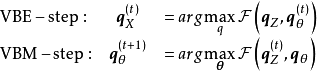



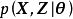



性質