廣義期望最大算法

廣義期望最大算法（Generalized Expectation Maximization）是數據不完全或者存在缺失變數的情況下參數估計的疊代算法。算法的每一次疊代是由期望(Expectation)和極大(Maximization)兩步操作構成，也是一種廣義的漸進逼近的最最佳化算法，在定義一個最最佳化函式後，主要分為以下兩步：1.根據參數調整模型（E步）；2.根據模型調整參數（M步）；E步和M步交替進行，直至得到最優解停止。

基本介紹

• 中文名：廣義期望最大算法
• 外文名：Generalized Expectation Maximization
• 基本領域：計算機科學
• 時間：1977年
• 屬性：最最佳化算法
• 使用範圍：數據缺失或不完全

基本思想

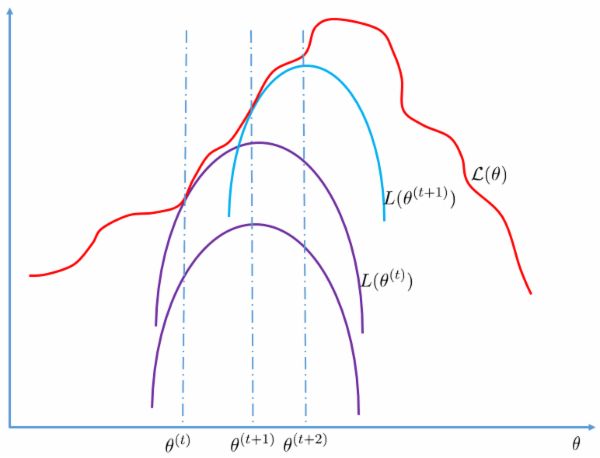
廣義期望最大算法的基本思想是首先在給出缺失數據初值的條件下估計出參數值，然後根據參數值估計出缺失數據的值；再根據估計出的缺失數據值對參數值進行更新，如此反覆疊代直至收斂。所謂存在缺失數據可以有兩種解釋，一種情況是由於問題本身的不合理或觀測條件的限制導致觀測數據存在缺失變數，另一種情況是缺失變數本身並不存在，但是觀測數據的似然函式最佳化比較複雜，而如果添加額外的隱(hidden)變數或潛在變數後的完全數據似然估計則比較簡單。

算法種類

狹義期望最大算法

EM（Expectatioin-Maximalization）算法即期望最大算法，被譽為是數據挖掘的十大算法之一。它是在機率模型中尋找參數最大似然估計的算法，其中機率模型依賴於無法觀測到的隱變數。最大期望算法經過兩個步驟交替進行計算，第一步是計算期望（E），也就是將隱藏變數象能夠觀測到的一樣包含在內，從而計算最大似然的期望值；另外一步是最大化（M），也就是最大化在E步上找到的最大似然的期望值從而計算參數的最大似然估計。M 步上找到的參數然後用於另外一個E步計算，這個過程不斷交替進行。對於信息缺失的數據來說，EM算法是一種極有效的工具。

K均值算法

K-means算法是很典型的基於距離的聚類算法，採用距離作為相似性的評價指標，即認為兩個對象的距離越近，其相似度就越大。該算法認為簇是由距離靠近的對象組成的，因此把得到緊湊且獨立的簇作為最終目標。

其中，k個初始類聚類中心點的選取對聚類結果具有較大的影響，因為在該算法第一步中是隨機的選取任意k個對象作為初始聚類的中心，初始地代表一個簇。該算法在每次疊代中對數據集中剩餘的每個對象，根據其與各個簇中心的距離將每個對象重新賦給最近的簇。當考察完所有數據對象後，一次疊代運算完成，新的聚類中心被計算出來。如果在一次疊代前後，J的值沒有發生變化，說明算法已經收斂。

算法過程如下：

1）從N個文檔隨機選取K個文檔作為質心。

2）對剩餘的每個文檔測量其到每個質心的距離，並把它歸到最近的質心的類。

3）重新計算已經得到的各個類的質心。

4）疊代2～3步直至新的質心與原質心相等或小於指定閾值，算法結束。

隱馬爾科夫模型

隱馬爾可夫模型是馬爾可夫鏈的一種，它的狀態不能直接觀察到，但能通過觀測向量序列觀察到，每個觀測向量都是通過某些機率密度分布表現為各種狀態，每一個觀測向量是由一個具有相應機率密度分布的狀態序列產生。所以，隱馬爾可夫模型是一個雙重隨機過程----具有一定狀態數的隱馬爾可夫鏈和顯示隨機函式集。自20世紀80年代以來，HMM被套用於語音識別，取得重大成功。到了90年代，HMM還被引入計算機文字識別和移動通信核心技術“多用戶的檢測”。HMM在生物信息科學、故障診斷等領域也開始得到套用。

在簡單的馬爾可夫模型（如馬爾可夫鏈），所述狀態是直接可見的觀察者，因此狀態轉移機率是唯一的參數。在隱馬爾可夫模型中，狀態是不直接可見的，但輸出依賴於該狀態下，是可見的。每個狀態通過可能的輸出記號有了可能的機率分布。因此，通過一個HMM產生標記序列提供了有關狀態的一些序列的信息。注意，“隱藏”指的是，該模型經其傳遞的狀態序列，而不是模型的參數；即使這些參數是精確已知的，我們仍把該模型稱為一個“隱藏”的馬爾可夫模型。隱馬爾可夫模型以它在時間上的模式識別所知，如語音，手寫，手勢識別，詞類的標記，樂譜，局部放電和生物信息學套用。

隱馬爾可夫模型可以被認為是一個概括的混合模型中的隱藏變數（或變數），它控制的混合成分被選擇為每個觀察，通過馬爾可夫過程而不是相互獨立相關。最近，隱馬爾可夫模型已推廣到兩兩馬爾可夫模型和三重態馬爾可夫模型，允許更複雜的數據結構的考慮和非平穩數據建模。

優缺點

優點

GEM算法的優點很明顯，主要表現在以下幾個方面：

1. 它所涉及理論的簡單化和一般性。
   
2. 在大多數情況下，它實質上是一個最佳化算法，並且能夠收斂到局部極值。
   
3. 許多的套用都能納入到EM算法的範疇，EM算法成為統計學上的—個標準工具。當完全數據來源於一個指數分布族時，極大似然估計計算就比較簡單，算法的每一個極大化的計算也比較簡單。
   

缺點

1. GEM算法會收斂到局部極值，但不保證收斂到全局最優解。

2. 對初值敏感：廣義期望最大算法通常需要一個好的、快速的初始化過程如矩方法得到的結果在GMM中，用 K-means聚類。

3. 適合的情況：缺失數據不太多時、數據維數不太高時。

模態分析中的套用

模態分析技術能夠有效的提取出固有頻率、模態振型、模態阻尼等模態參數，為解決機械振動方面的問題提供了重要手段。在傳統的模態分析方法中，實驗模態分析占據著主流地位，得到了廣泛的套用。實驗模態分析方法的優點是已知輸入信號和輸出信號，可以較為準確的求解出系統的模態參數。然而，在實際工程套用中，各種機械設備所受工作載荷和外界環境的激勵，這些因素的輸入信號很難測量。因此，工作模態分析方法憑藉其只通過測量系統的輸出回響來進行模態參數的識別的優勢，如今在工程實際中越來越被重視。

期望最大化算法（算法）是一種用於最大可能性估計的全目標算法，在統計學上擁有一些最佳屬性。期望最大化算法在計算最大似然估計中套用的非常廣泛，它的使用過程中包括了步驟（估算條件期望）和步驟（最大化條件期望），如此形成一個循環疊代的步驟，最終達到收斂。期望最大化算法在很多領域中都有套用，如心理學，環境學，天文學等。當使用期望最大化算法來計算模態參數時，算法初始值的選取非常重要，初始值選取的合適與否直接決定了識別結果的精度。在本文的研宄中，期望最大化算法的初始值選取隨機子空間法（法）的結果，因為隨機子空間法得出的分析結果是接近全局最大值的，因此在此基礎上再使用算法可以將結果收斂到全局最大值上，防止結果在局部最大值上收斂。

此外，套用期望最大化算法計算模態參數時，還可以選擇隨機點作為其初始值，此種方法較為輕鬆、快捷，每個隨機起點提供了一組估計模型，如果一個模式是由多個起始點表達的，可以作為系統的模型。