用疊代的鬆弛算法對線性最小二乘估計的一種改進。線性最小二乘估計在模型誤差為相關噪聲時是有偏估計,即其估計值存在偏差。這時採用廣義最小二乘估計能獲得較精確的結果。
基本介紹
- 中文名:廣義最小二乘估計
- 外文名:Generalized least squares estimation
- 性質:估計
- 類型:現代詞
原理,案例,特性,套用,實現,
原理
廣義最小二乘估計就是使估計準則J為極小的參數估計。多項式A(z-1)、B(z-1)和C(z-1)的係數都是未知的,所以不能用一個線性算法獲得廣義最小二乘估計。
案例
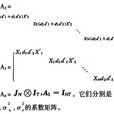
假設所討論的單輸入單輸出系統的差分方程模型是
式中{uk}和{yk}分別是輸入和輸出序列:
和
是運算元多項式,它們的係數是需要通過估計來求出的未知數;z-1是單位延遲運算元;{ek}是誤差序列,它是零均值平穩相關噪聲序列。為了進行廣義最小二乘估計可以從形式上把ek變換成廣義最小二乘估計,這裡廣義最小二乘估計廣義最小二乘估計,它的係數也是未知的。如果{ek}具有有理譜密度,則可把{εk}當作白噪聲序列來處理。
特性
廣義最小二乘估計採用疊代的鬆弛算法:先行固定C(z-1),估計A(z-1)和B(z-1),使J 趨於極小;然後固定A(z-1)和B(z-1),估計C(z-1),使 J 趨於極小。如此反覆疊代,直至估計值收斂。這時每步只進行簡單的線性最小二乘估計運算,疊代的初值取扗(z-1)=1。
套用
這種算法也可推廣到多輸入多輸出系統,並且有相應的近似遞推估計算法。當誤差{ek}為正態噪聲序列時,這種算法還可以解釋為極大似然估計的鬆弛算法。