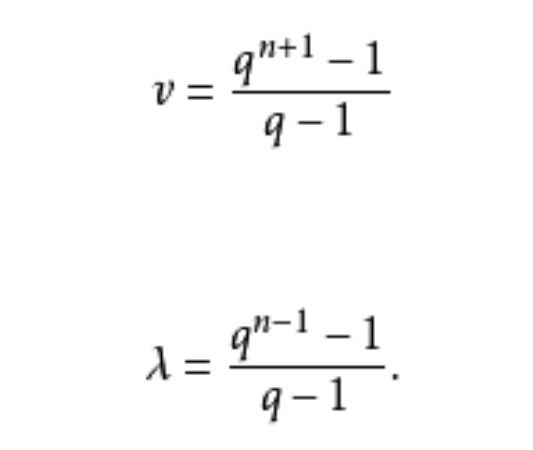有限射影空間

有限射影空間(finite projective space)是一類組合構形，是滿足以下公理的有限點集上的關聯繫統：1.對兩相異點，有且僅有一條線含這兩個點；2.若A，B，C是不共線的三點，D是含A，B的線上異於A的點，E是含A，C的線上異於A的點，則含D，E的線與含B，C的線含一個公共點F；3.每條線至少含三個相異點。

基本介紹

• 中文名：有限射影空間
• 外文名：finite projective space
• 所屬學科：數學
• 所屬問題：組合學（組合設計）
• 簡介：一類組合構形

基本介紹

若射影空間的某個子集在含一條線上的兩個點時必含這條線上所有的點，則稱該子集為子空間。將點稱為零維子空間，線稱為1維子空間，由此可歸納地定義子空間的維數，若子空間X_n-1的維數為n-1，P是射影空間中不屬於X_n-1的一點，將含P及X_n-1中任一點的所有線上的點的全體記為X_n，則X_n是子空間，其維數定義為n，在n維射影空間中，2維子空間稱為平面，n-1維子空間稱為超平面，若某條線上含q+1個點，則每條線上都含q+1個點，此時稱射影空間是q階的，q階n維射影空間記為PG(n，q)，將q元有限域上n+1維向量空間中的一維子空間取作“點”，2維子空間取作“線”，便得到n維射影空間PG(n，q)的一個例子.這樣的“點”可用一個n+1維的非零向量(x₁，x₂，…，x_n+1)表示，當λ為有限域中非零元時，向量λ(x₁，x₂，…，x_n+1)將表示同一個“點”.稱(x₁，x₂，…，x_n+1)為射影空間中點的齊次坐標，PG(n，q)中共有

個點，一個超平面含k=(q-1)/(q-1)個點,若將一個PG(n，q)中所有超平面取作區組，則得到一個(v，k，λ)-BIBD，其中

當n≥3時，PG(n，q)在同構的意義下是惟一的，但是，當n=2時，存在不同類型的射影平面。

平面上的點(x₁，x₂)，若令

則便是二維射影空間的坐標，而且對於不為零的任意常數ρ，有

即和表示同一個點，可把上面的討論推及到高維空間，例如(x₁，x₂，x₃)是三維空間的點的坐標，引進

則是三維射影空間的坐標，還可以將它推廣到一般的情況。

二維的射影幾何

GF(p)是含有p個元素的域，其中p是素數。GF(p)上m-1維射影空間的點用

來表示，除(0，0，…，0)外共個，只是

看做是與是相同的點，其中，且，所以m-1維GF(p)域上射影空間的點數為

設P₁和P₂是m-1維空間中的任意兩個點，令

表示P₁和P₂連線上的點,其中且不同時為0，故有p-1種配合方案，但有p-1次重複，故P₁和P₂點連線上的點數為

其中包含P₁和P₂點在內，當p=2時，每條連線上有3個點，當p=4時有4個點。

有限域上的射影空間

可將上面的討論一般化，推廣到任一有限域F上，假定x_i∈F，i=0，1，2，...，n，向量

的空間用PG(n，F)表示，PG(n，F)的點指的是向量集合：

其中x=≠0，b為F的所有元素，更一般地，設是k+1個獨立向量，則向量集合：

的空間是k維子空間S_k，其中b_i∈F，i=1，2，…，k，特別是n-1維子空間稱為超平面，不難證明：超平面的交是n-2維的子空間。

若，所有滿足

的向量的集合是一個超平面。反之，所有的超平面都可用式(1)來定義。和確定的是同一超平面，s≠0。

若域F是有限域GF(p)，令q=p，則存在q個向量：

其中q-1個非零向量，定義q-1個點，i=0，1，2，…，n，由於

和

表示同一個點，故實際上有

個點，類似地，因為和確定同一個超平面，故有v個超平面，可證一超平面是n-1維子空間，有

個不同的點。

一般地t維空間由t+1個獨立向量及，i=0，1，2，…，t所定義的

所確定，除去零向量，應有

個不同的點，兩超平面的交為n-2子空間，故，可得如下定理。

定理以PG(n，p’)的超平面作為區組，點作為對象，構成如下一對稱的區組設計：