最短路徑問題是組合最佳化領域的經典問題之一,它廣泛套用於計算機科學、交通工程、通信工程、系統工程、運籌學、資訊理論、控制理論等眾多領域。Dijkstra算法是經典的最短路徑算法。
基本介紹
- 中文名:最短路徑問題
- 外文名:shortest path problem
- 實質:找出圖中兩個頂點間的最短路徑
- 套用領域:計算機科學、交通工程、通信工程等
相關算法
Dijkstra算法
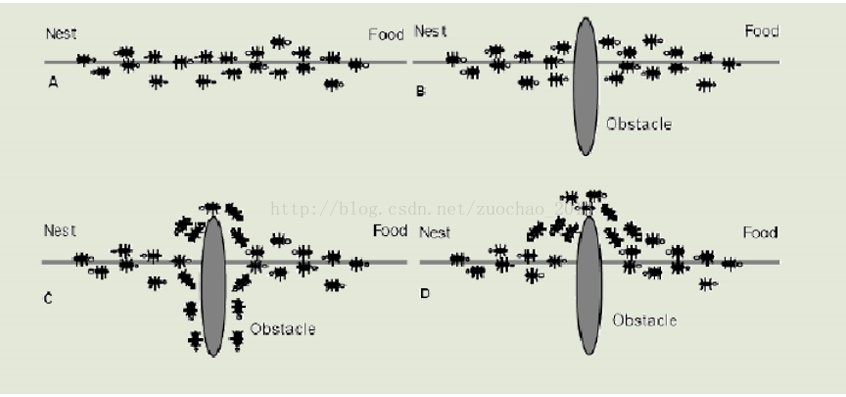
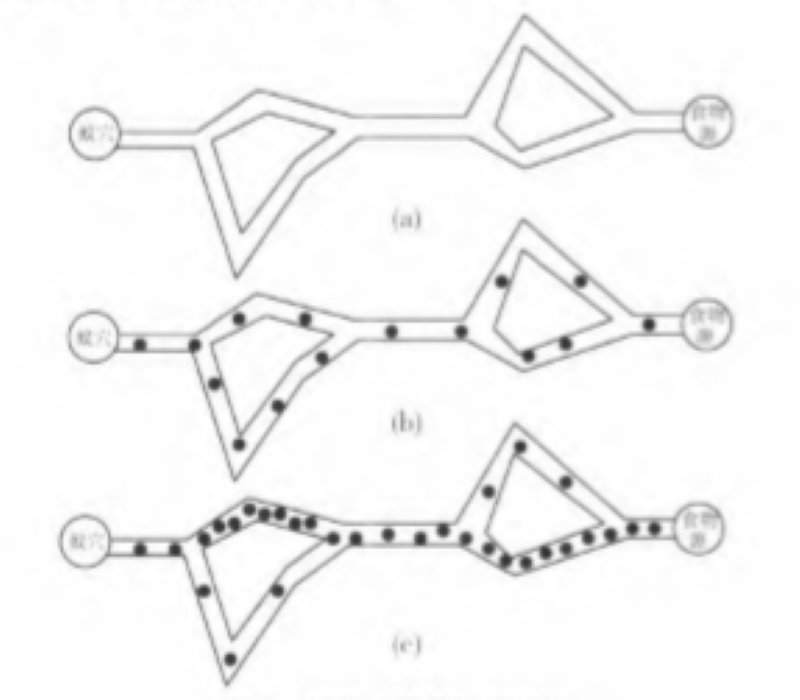
蟻群算法
最短路徑問題是組合最佳化領域的經典問題之一,它廣泛套用於計算機科學、交通工程、通信工程、系統工程、運籌學、資訊理論、控制理論等眾多領域。Dijkstra算法是經典的最短路徑算法。

最短路徑問題是組合最佳化領域的經典問題之一,它廣泛套用於計算機科學、交通工程、通信工程、系統工程、運籌學、資訊理論、控制理論等眾多領域。Dijkstra算法是經典的最短路徑算法。相關算法 Dijkstra算法 Dijkstra算法是經典的最短路徑算法,其...
用於解決最短路徑問題的算法被稱做“最短路徑算法”, 有時被簡稱作“路徑算法”。 最常用的路徑算法有:Dijkstra算法 SPFA算法\Bellman-Ford算法 Floyd算法\Floyd-Warshall算法 Johnson算法 A*算法 所謂單源最短路徑問題是指:已知圖G=...
最短路徑問題是圖論研究中的一個經典算法問題,旨在尋找圖(由結點和路徑組成的)中兩結點之間的最短路徑。算法具體的形式包括:(1)確定起點的最短路徑問題- 即已知起始結點,求最短路徑的問題。適合使用Dijkstra算法。(2)確定終點的...
最短路徑問題 最短路徑問題是圖論研究中的一個經典算法問題, 旨在尋找圖(由結點和路徑組成的)中兩結點之間的最短路徑。 算法具體的形式包括:確定起點的最短路徑問題 - 即已知起始結點,求最短路徑的問題。確定終點的最短路徑問題 ...
給定一個帶權有向圖G=(V,E),其中每條邊的權是一個實數。另外,還給定V中的一個頂點,稱為源。要計算從源到其他所有各頂點的最短路徑長度。這裡的長度就是指路上各邊權之和。這個問題通常稱為單源最短路徑問題。Dijkstra算法 ...
求解單源最短路徑問題可以採用Dijkstra算法,時間複雜度為O(|V|^2)。Dijkstra算法可以使用斐波那契堆、配對堆等支持Decrease-Key操作的數據結構來進一步最佳化,最佳化後的時間複雜度為O(|E|+|V|log|V|)。Dijkstra只可求無負權的最短路徑...
最大流量問題,簡稱F問題。最短路徑問題,簡稱S問題。任務分配問題,又稱指派問題,簡稱A問題。生產計畫問題,又稱日程計畫問題,簡稱CPS問題。如把產地稱為源(發點),銷地稱為匯(收點),則任務分配問題、生產計畫問題等運輸型問題的...
《隨機模糊時變網路最短路徑問題研究》是依託天津理工大學,由黃瑋擔任項目負責人的青年科學基金項目。項目摘要 不確定環境下的時變網路最短路徑問題在通信、計算機、智慧型交通等多個領域有著廣泛的套用,其中時變網路中的不確定性往往被...
ESP(Euclidean Shortest Path )即歐式最短路徑,ESP問題是計算機圖形學裡的一種典型問題。ESP(EuclideanShortestPath)即歐式最短路徑,ESP問題是計算機圖形學裡的一種典型問題。主要目的是在給定一系列的障礙下,找出兩點之間的最短路徑...
本課內容是人教版八年級下冊第十三章《軸對稱》中的課題學習最短路徑問題,這個內容是解答題的常考知識點,對於學生是個難點,利用微課視頻可以幫助學生理解和掌握。設計思路 本課從教材上的造橋選址問題入手,通過幾何畫板動態演示,一...
《勾股定理的套用—最短路徑問題》是臨江市光華中學提供的微課課程,主講教師是王桂明。課程簡介 學會把幾何體表面展開成平面圖形,找到最短路徑。 通過展開圖形,構建直角三角形,運用勾股定理求出最短路徑。 過程與方法 通過動手操作,...
《沿圓錐體側面的最短路徑問題》是伊金霍洛旗四中學校提供的微課課程,主講教師為徐曉梅 。課程簡介 人教版義務教育課程標準實驗教科書九年級上冊 第24章 圓 《24.4——弧長和扇形面積》微教學設計 新課標指出:”數學教育不僅要使學生...
《人教版八年級數學上冊:最短路徑問題-微課堂》是成都西藏中學提供的微課課程,主講教師為敬曉萍。課程簡介 本節課首先帶學生進行回顧複習,讓學生從圖片上獲得感性認識“從A地到B地有3條可供選擇,哪條路最近?”,從而理解運用線段最...
最短路徑分配法是指按所有出行者都選取出行最短的路線從出發點到目的地的原則分配交通量。“非平衡分配模型”的一種,是其他各種交通分配方法的基礎。隨著道路建設的發展,最短出行距離被最短交通阻抗取代,最常用的是出行時間。基本假定...
《改進的Dijkstra最短路徑算法及其套用研究》是王樹西、吳政學撰寫的一篇論文。論文摘要 求最短路徑是一個套用很廣泛的問題。求最短路徑的算法有很多,公認較好的算法是Dijkstra標號法。但實驗結果表明,Dijkstra標號法有需要改進的地方:①其...
這樣可以極大的最佳化普通的廣度優先的路徑搜尋,但是搜尋準確度受到估價函式的影響,其結果不一定是最短路徑。以上方法雖然可以實現最短路徑搜尋問題,但存在如下缺點和不足:1)搜尋效率低,搜尋結果與效率難以得到均衡;2)處理過程複雜,...
大量實證表明:出行者在行程時間不確定的情況下更傾向於選擇可靠度高的路徑,即可靠最短路徑。因此,很有必要研究隨機網路中的可靠最短路徑問題。由於可靠最短路徑具有不可加性(即路徑阻抗不等於路段阻抗之和),不能直接採用傳統的最短...
以問題串的形式激發學生思維訓練“沿長方體該怎樣爬行呢。” (二)問題呈現 引發學生思考:1.爬行路徑由幾種不同的爬法。 2.如何轉化求最短路徑。(三)變式訓練 (四)方法總結 步驟和方法: 1.利用轉化思想:將折面轉化為平面...
經典的圖論與計算機算法的有效結合,使得新的最短路徑算法不斷湧現。目前提出的最短路徑算法中,使用最多、計算速度比較快,又比較適合於計算兩點之間的最短路徑問題的數學模型就是經典的Dijkstra算法。該算法是典型的單源最短路徑算法,由...
《用尺規作圖解決將軍飲馬問題》是寧津縣第一實驗中學提供的微課課程,主講教師是田文慶。課程簡介 在電子白板上用希沃軟體中尺規工具解決將軍飲馬問題---最短路徑問題。代替傳統的實物三角板、尺子、圓規等,更加直觀,解決了教室粉塵問題。
通過內插方法,計算出路徑節點與格線上的所有交叉點集,通過格線化處理,計算與格線交叉點集,沒有在格線上有交叉的不納入計算範圍,這樣內插計算有利於解決颱風歷史數據中路徑節點時空分布不均勻的問題,使要計算各路徑點的權重分配平均,...
所以本節課的學習不僅具備承上啟下的作用,更能直擊中考考點——最短路徑問題。 二、學情分析 (一)學生的已有基礎: 知識基礎:通過本章前一節的學習,學生已經掌握了勾股定理並能運用勾股定理求線段長度,並且掌握了“豐富的圖形...
迪傑斯特拉算法(Dijkstra)是由荷蘭計算機科學家狄克斯特拉於1959年提出的,因此又叫狄克斯特拉算法。是從一個頂點到其餘各頂點的最短路徑算法,解決的是有權圖中最短路徑問題。迪傑斯特拉算法主要特點是從起始點開始,採用貪心算法的策略,...
貝爾曼-福特算法(Bellman-Ford)是由理察·貝爾曼(Richard Bellman) 和 萊斯特·福特 創立的,求解單源最短路徑問題的一種算法。有時候這種算法也被稱為 Moore-Bellman-Ford 算法,因為 Edward F. Moore 也為這個算法的發展做出了...
現已發現的運輸型問題有以下6類:①一般運輸問題,又稱希契科克運輸問題,簡稱H問題。②網路運輸問題,又稱圖上運輸問題,簡稱T問題。③最大流量問題,簡稱F問題。④最短路徑問題,簡稱S問題。⑤任務分配問題,又稱指派問題,簡稱A問題。...
魚型問題 魚型問題 路由決策一般基於簡單度量(如跳數或時延) 原則,採用最短路徑算法,這種簡化做法使路由技術獲得了很好的伸縮性,但在資源分配和最佳化等方面卻沒有提供足夠的支持。這可以通過著名的“魚型問題”來說明。網路拓撲形狀...
