曼戈爾特函式(von Mangoldt function)是曼戈爾特提出來的以他的名字命名的函式,也稱第二切比雪夫函式,它在素數分布論中有重要作用。曼戈爾特函式記為Λ(n)。
基本介紹
- 中文名:曼戈爾特函式
- 外文名:von Mangoldt function
- 提出者:曼戈爾特
- 別名:第二切比雪夫函式
- 符號:Λ(n)
- 相關概念:素數定理、麥比烏斯反演公式等
定義



 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
 |  |  |  |  |  |  |  |
相關定理










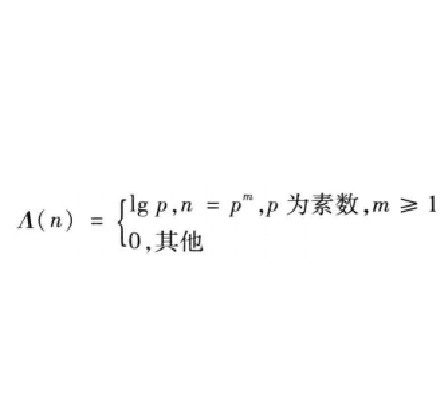
曼戈爾特函式(von Mangoldt function)是曼戈爾特提出來的以他的名字命名的函式,也稱第二切比雪夫函式,它在素數分布論中有重要作用。曼戈爾特函式記為Λ(n)。



 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
 |  |  |  |  |  |  |  |










曼戈爾特函式(von Mangoldt function)是曼戈爾特提出來的以他的名字命名的函式,也稱第二切比雪夫函式,它在素數分布論中有重要作用。曼戈爾特函式記為Λ(n)。定義對每一個整數 ,我們定義是的牟比烏斯變換,...
曼戈爾特函式是重要的數論函式之一。曼戈爾特函式Λ(n)定義為:如Λ(1)=0,Λ(2)=ln 2,Λ(3)=ln 3,Λ(4)=ln 2等。 曼戈爾特函式有如下性質: 1.Λ(n)不是積性函式. 2.Λ(n)=μ(n)ln. ...
5 曼戈爾特函式Λ(n)(11)6 麥比烏斯函式的兩個簡單性質(12)7 麥比烏斯函式的積性(14)8 麥比烏斯反演定理(17)9 麥比烏斯反演公式的推廣(19)10 麥比烏斯變換的多種形式(20)第2章 套用舉例 1 麥比烏斯函式與分圓多項式(22)2 ...
曼戈爾特函式(von Mangoldt function)是曼戈爾特提出來的以他的名字命名的函式,也稱第二切比雪夫函式,它在素數分布論中有重要作用。曼戈爾特函式記為Λ(n)。定義 對每一個整數 ,我們定義 是 的牟比烏斯變換,而 是 的牟比烏斯...
是一個狄利克雷L函式。還有:其中φ(n) 是歐拉函式。以及:其中 σₐ(n) 是因數函式。其他關於因數函式d=σ₀的等式還有:對於Re(s)>1,ζ函式的對數由下式給出:其中 為馮·曼戈爾特函式。其導數由下式給出:更廣泛的...
此公式是塞爾伯格((Selberg,A.)將曼戈爾特函式通過默比烏斯反演公式而導出,塞氏還巧妙地運用部分求和法由此公式導出B(x) ^}x,首次成功地不用函式論方法而證明了素數定理。此公式載於塞氏的論文《等差數列的素數定理的初等證明》中。
§4.5 曼戈爾特函式Λ(n) §4.6 麥比烏斯函式的兩個簡單性質 §4.7 麥比烏斯函式的積性 §4.8 麥比烏斯反演定理 §4.9 麥比烏斯反演公式的推廣 §4.10 麥比烏斯變換的多種形式 第5章 套用舉例 §5.1 麥比...
5 曼戈爾特函式// 12 6 麥比烏斯函式的兩個簡單性質 // 13 7 麥比烏斯函式的積性 // 11 8 麥比烏斯反演定理 // 17 9 麥比烏斯反演公式的推廣 // 18 10 麥比烏斯變換的多種形式 // 19 第二章 套用舉例 // 21 1 麥比...
