曲率向量

若某向量模數等於研究點處給定曲線的曲率，而該向量的方向與該點處曲線的主法線方向相同，則稱該向量為曲率向量。

基本介紹

• 中文名：曲率向量
• 外文名：curvature vector
• 所屬學科：數學
• 所屬問題：微分幾何學（曲線和曲面）
• 相關概念：曲率，曲率圓，曲率半徑等

基本介紹

曲率(curvature)是表示曲線彎曲程度的一個運動不變數。設曲線的單位切向量為，稱

為曲線在s處的曲率，其中是切向量和之間的夾角。曲率度量了曲線上相鄰兩點的切向量的夾角關於弧長的變化率，它刻畫了曲線彎曲程度。如曲率k恆為0的曲線是直線，稱為該曲線的曲率向量，當時，曲率k的倒數稱為曲線在s處的曲率半徑。當曲線用一般參數表示，即時，曲率的計算公式為

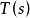
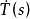
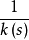
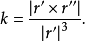
曲率指表明曲線在某一點的彎曲程度的數值。對於平面或空間曲線上的一點P，取它的兩個鄰近點Q和R，過這三點作一個圓。當Q、R沿曲線接近P時，如果這個圓有一個極限位置，則稱這個極限圓為曲線在點P的“曲率圓”，它的半徑稱為“曲率半徑”，曲率半徑的倒數稱為“曲率”。曲率愈大，表示曲線的彎曲程度愈大。反之，曲率愈小，表示曲線的彎曲程度愈小。在近似於直線的曲線上，每一點的曲率就愈小，由此推知直線上各點的曲率是無限小，所以直線就被看作是曲率無限小的曲線。這樣，直線和曲線雖然在初等數學裡是兩個不同的數學概念，但在這裡卻表現為可以互相轉化，直線和曲線的對立就在曲率無窮小的條件下統一起來了。

法曲率向量與測地曲率向量

設M為中的維超曲面，為其參數表示，為M上的一條曲線，s為弧長參數，的曲率向量定義為

而稱為曲線在s處的法曲率向量，

稱為法曲率，

稱為測地曲率向量。