基本介紹
圖形的位置關係和數量關係,是幾何研究的兩種基本關係。角有位置相關的角,也有數量相關的角。位置相關的角,如
對頂角、同位角、
內錯角、
同旁內角、鄰角等,數量相關的角是
餘角與
補角等,數量都相關的角是
鄰補角。
同旁內角是位置相關的角,但它們互補時,又是數量相關的角。
數量相關的角舉例
兩個角的和等於一直角(等於90°)時, 就說這兩個角互為餘角(簡稱互余,其中一個角是另一個角的餘角)。由此可見,互為餘角有兩個基本特徵:第一是有兩個角;第二是它們的和等於一直角(等於90°)。如圖1,∠1=30°,∠2=60°,∠1、∠2是兩個角,符合第一個基本特徵;∠1與∠2之和等於90°,即∠1+∠2=90°,符合第二個基本特徵。 所以∠1、∠2互為餘角。∠1是∠2的餘角,∠2也是∠1的餘角。
 圖1
圖1 圖2
圖2兩個角的和等於一平角(等於180°) 時,就說這兩個角互為補角 (簡稱互補, 其中一個角是另一個角的補角)。由此可見, 互為補角有兩個基本特徵:第一是有兩個角;第二是它們的和等於一平角。如圖2。∠3+∠4=180°,所以∠3、∠4互為補角。∠_3是∠4的補角,∠4也是∠3的補角。
關於兩個角互為餘角和互為補角兩個概念,是常用的概念,不要把這兩個概念混淆。這兩個概念的共同特徵是兩個角,不同的特徵是兩個角互為餘角時,它們的和等於90°。兩個角互為補角時,它們的和等於180°。互余、互補是指兩個角的數量間的關係,與這個角的位置無關。無論∠1與∠2在什麼位置,它們的和等於90°,都叫互為餘角;無論∠3和∠4在什麼位置,它們的和等於180°,都叫做互為補角。
將一個角的一邊反向延長,這條反向延長的線與這個角的另一邊構成一個角,它和原來的角叫做互為鄰補角。互為鄰補角有三個特徵:第一是要有兩個角;第二是它們有共同的頂點和一條公共邊;第三是它們之和等於一平角。圖2右側的圖中,∠3與∠4有一條公共邊,它們的位置相鄰且互補, 所以是互為鄰補角。圖2左側的圖中,∠3和∠4互補而不相鄰,所以不是互為鄰補角。
| 定 義 | 圖 示 | 有關定理 |
互為餘角 | 兩個角的和等於90°,即α+β=90° |  互餘角 互餘角 | 同角(或等角)的餘角相等 |
互為補角 | 兩個角的和等於180°,即α+β=180° | 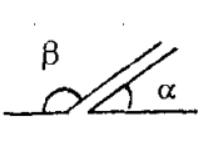 互補角 互補角 | 同角(或等角)的補角相等 |
互為鄰補角 | 有公共頂點和一條公共邊,另一條邊互為延長線 |  鄰補角 鄰補角 | |
 圖1
圖1 圖2
圖2 互餘角
互餘角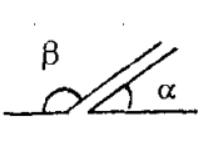 互補角
互補角 鄰補角
鄰補角
