基本介紹
- 中文名:數乘向量
- 外文名:scalar multiplication of vectors
- 所屬學科:數學
- 簡介:數量與向量的乘法運算
- 相關概念:共線向量
基本介紹









數乘向量的相關性質





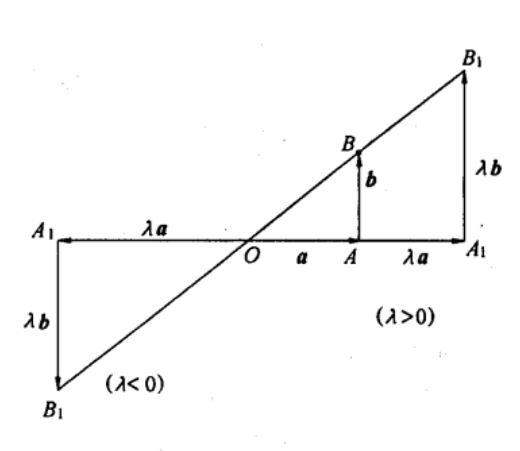














平行向量數乘運算 實數λ與向量 的積是一個向量,這種運算叫做向量的數乘,記作 , 。當λ > 0時, 的方向和 的方向相同,當λ < 0時, 的方向和 的方向相反,當λ = 0時, = 0,方向任意。
平面向量數乘 實數λ與向量a的積是一個向量,這種運算叫做向量的數乘,記作λa。當λ>0時,λa的方向和a的方向相同,當λ<0時,λa的方向和a的方向相反,當λ = 0時,λa=0。用坐標表示的情況下有:λAB=λ(x2-x1,y2-y1)...
數乘向量的消去律:① 如果實數λ≠0且λa=λb,那么a=b。② 如果a≠0且λa=μa,那么λ=μ。需要注意的是:向量的加減乘(向量沒有除法)運算滿足實數加減乘運算法則。數量積 定義:已知兩個非零向量a,b,作OA=a,OB=b,...
1.3向量的數乘與向量共線定理 本講達標訓練 第2講平面向量的基本定理及坐標運算 2.1平面向量的基本定理及其套用 2.2平面向量的坐標運算 本講達標訓練 第3講平面向量的數量積及其套用 3.1平面向量的數量積及其性質 3.2平面向量數量...
向量組構造的增廣矩陣 表示 ,稱為計算式的集合簡化形式。構成係數列向量的分量因為公共解集之間。構造向量後可實現向量計算(向量加法與數乘),例如向量組的線性組合(複合計算):向量的線性組合計算 &向量的表示方法.1符號表示方法 ①...
向量的大小是相對的,在有需要時,會規定單位向量,以其長度作為1。每個方向上都有一個單位向量。向量之間可以如數字一樣進行運算。常見的向量運算有:加法,減法,數乘向量以及向量之間的乘法(數量積和向量積)。加法與減法 向量的加法...
一、數乘向量47 二、向量共線的判定50 習題三52 第四節平面向量分解定理53 習題四56 第五節直角坐標系下向量的運算57 一、向量的直角坐標57 二、向量的坐標運算58 三、向量坐標與點坐標59 習題五61 第六節分點坐標公式61 一、...
第10章向量與複數251 10 1向量的概念251 習題101253 10 2向量加減法、數乘向量253 10 2 1向量的加法253 10 2 2向量的減法255 10 2 3數乘向量256 習題102258 10 3向量的坐標運算258 10 3 1向量的坐標運算258 10 3 2平面...
第7章 向量 一 向量的概念及其運算 7.1 向量的概念和向量的幾何表示 7.2 向量的加法與減法 7.3 數乘向量 二 向量的坐標 7.4 平面向量的坐標·用坐標作向量的運算 7.5 平面向量的坐標與點的坐標的關係 7.6 線段的中點坐標...
第2題 數乘向量關係好,等價轉化得方程 第3題 動點軌跡方程繪,八方聯繫法不同 第4題 橢圓與圓相伴生,伸長壓縮變換成 第2節 要素多變幻,直線曲線聯——直線與圓錐曲線的綜合問題 第5題 條件紛繁不尋常,一參貫穿全局活 第6題 動...
1.2.2 向量的數乘 1.3 平面向量的套用 1.4 習題課 小結 第二章 常用邏輯語言 2.1 命題及其關係 2.2 充要條件 2.3 簡單的邏輯聯結詞 2.4 習題課 小結 第三章 直線和平面 3.1 平面及其性質 3.1.1 平面 3.1.2 ...
的向量 4.1 向量的類型 4.2 平面和空間中的向量運算 4.2.1 向量的加減 4.2.2 向量的數乘 4.2.3 向量與向量的數量積 4.2.4 向量與向量的向量積 4.3 平面和空間的向量空間 4.3.1 平面和空問向量的線性相關性 4.3.2 平面向量...
1.2.2 向量的數乘 10 1.2.3 基本運算法則 11 1.3 線性組合與線性相關 12 1.3.1 混合顏色 13 1.3.2 線性組合 15 1.3.3 線性相關和線性無關 17 1.3.4 線性相關和線性無關的例題 18 1.3.5 升...
1.2.2 向量的數乘 1.3 平面向量的套用 1.4 習題課 小結 第二章 常用邏輯語言 2.1 命題及其關係 2.2 充要條件 2.3 簡單的邏輯聯結詞 2.4 習題課 小結 第三章 直線和平面 3.1 平面及其性質 3.1.1 平面 3.1.2 ...
1.e是單位向量,則e·a=a·e=|a|cos 2.a⊥b⇔a·b=0(a,b為非零向量);3.a·a=|a|或|a|= ;4.cos= ;5.|a·b|≤|a||b|;說明:(1)兩個向量的數量積不同於它們的加減運算或數乘,其結果不是向量而...
第六章 複數與向量 1.複數的基本性質 1·1 虛數單位 1·2 複數的定義 1·3 複數的四則運算 1·4 共軛複數 1·5 複數的模 1·6 複數的極坐標形式(複數的三角表示式)1·7 複數的旋轉 2.複數與圖形 2·1 複數的四則運算...
(4)線性變換類。例如:矩陣特徵值變換,Ax=tx( 矩陣A,特徵值t,向量x),將向量的矩陣乘用向量的數乘代替。3數據元表示形式化簡 (5)數據元用代數分解式表示或變數替換。例如:可對角化矩陣用相似變換式表示,可在求冪等運算中...
