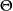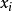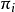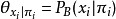基本介紹
- 中文名:改進樸素貝葉斯
- 外文名:Naive Bayes
- 樸素貝葉斯:屬性條件獨立性假設
- 改進:正則化;考慮屬性間依賴關係
- 實例:半樸素貝葉斯分類器;貝葉斯網路
- 套用:分類
樸素貝葉斯,正則化,半樸素貝葉斯分類器,貝葉斯網路,
樸素貝葉斯
為了避開這個障礙,樸素貝葉斯分類器採用了“屬性條件獨立性假設”:對已知類別,假設所有屬性相互獨立。換言之,假設每個屬性獨立地對分類結果發生影響。
但在現實任務中,這個假設往往很難成立,於是人們嘗試對屬性條件獨立性假設進行一定程度的放鬆,由此產生了一類“半樸素貝葉斯分類器”的學習方法。
正則化
在樸素貝葉斯中,計算聯合機率時,為了避免其他屬性攜帶的信息被訓練集中從未出現的屬性值“抹去”,在估計機率值時通常要進行“平滑”,常用“拉普拉斯修正”。具體來說,令N表示訓練集D中可能的類別數,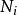 表示第i個屬性可能的取值數,則
表示第i個屬性可能的取值數,則
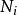

半樸素貝葉斯分類器
半樸素貝葉斯的基本思想是:適當考慮一部分屬性間的相互依賴信息,從而既不需要進行完全聯合機率計算,又不至於徹底忽略了比較強的相互依賴關係。“獨依賴估計”是半樸素貝葉斯分類器中最常用的一種策略。顧名思義,所謂“獨依賴”,就是假設每個屬性在類別之外最多依賴於一個其他屬性。
最直接的做法是假設所有屬性都依賴於同一個屬性,稱為“超父”(super-parent),然後通過交叉驗證等模型方法來確定超父屬性,由此形成了SPODE(Super-Parent ODE)方法。
TAN(Tree Augmented naive Bayes)則是在最大帶權生成樹(maximum weighted spanning tree)的基礎上,通過以下步驟將屬性間依賴關係約簡為如圖所示(c)的樹形結構:

上圖是樸素貝葉斯與兩種半樸素貝葉斯分類器所考慮的屬性關係,其中,(a)是NB,(b)是SPEDE,(c)是TAN
步驟:
1)計算兩個屬性之間的條件互信息(conditional mutual information)
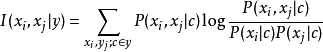
2)以屬性為結點,構建完全圖,任意兩個結點之間邊的權重設為

3)構建此完全圖的最大權生成樹,挑選根變數,將邊置為有向。
4)加入類別結點 y,增加從 y 到每個屬性的有向邊。
容易看出,條件互信息 刻畫了屬性
刻畫了屬性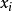 和
和 在已知類別情況下的相關性,因此,通過最大生產樹算法,TAN實際上保留了強相關屬性之間的依賴性。
在已知類別情況下的相關性,因此,通過最大生產樹算法,TAN實際上保留了強相關屬性之間的依賴性。


貝葉斯網路
具體來說,一個貝葉斯網B由結構G和參數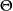 兩部分構成,即
兩部分構成,即 。網路結構G是一個有向無環圖,其每個結點對應一個屬性,若兩個屬性有直接依賴關係,則它們由一條邊連線起來;參數
。網路結構G是一個有向無環圖,其每個結點對應一個屬性,若兩個屬性有直接依賴關係,則它們由一條邊連線起來;參數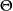 定量描述這種依賴關係。假設屬性
定量描述這種依賴關係。假設屬性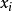 在G中的父結點集為
在G中的父結點集為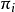 ,則
,則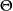 包含了每個屬性的條件機率表
包含了每個屬性的條件機率表