《摺疊中的數學問題》是東明學校提供的微課課程,主講教師為杜春英。
基本介紹
- 中文名:摺疊中的數學問題
- 提供學校:東明學校
- 主講教師:杜春英
- 類 別:微課
《摺疊中的數學問題》是東明學校提供的微課課程,主講教師為杜春英。
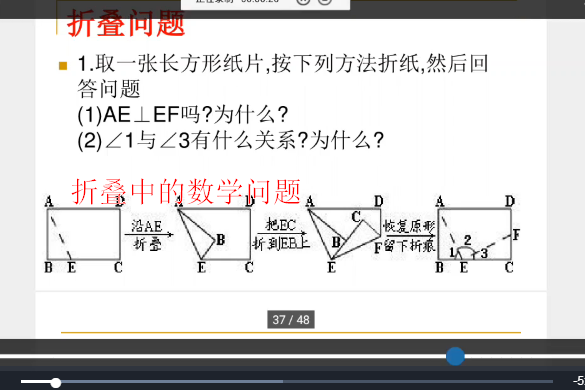
《摺疊中的數學問題》是東明學校提供的微課課程,主講教師為杜春英。課程簡介摺疊長方形紙片,會得到一些邊和角的關係,從而得到一些有趣的數學問題。1設計思路摺疊問題在國中數學中出現的頻率比較高,本微課主要是講述摺疊產生的線段、...
摺紙數學指的是對摺紙藝術從數學的角度加以研究。例如,研究某個特定的紙模型的可展性以及使用摺紙來解數學方程。定義 摺紙數學是指對摺紙藝術從數學的角度加以研究。比如,研究某個特定的紙模型的可展性(研究該模型是否可以攤平而無須把它弄破)以及使用摺紙來解數學方程。解釋 某些經典幾何作圖問題例如三等分角,...
1.2006年論文《數學競賽中的摺疊、展開和拼接問題》在天津師範大學主辦的《中等數學》第四期上發表 2.2008年論文《對數列通項最值問題的一個解法的思考》在華中師範大學主辦的《數學通訊》第15期上發表 3.2008年論文《利用定積分和曲邊梯形面積的關係解題》在曲阜師範大學主辦的《中學數學雜誌》第5期發表 4....
《周計畫:中考數學壓軸題高效訓練(摺疊與旋轉)》是2019年華東理工大學出版社出版的圖書,作者是劉弢。內容簡介 《周計畫:中考數學壓軸題高效訓練》系列為國中數學專項的壓軸題訓練,按內容細分為三角形與四邊形、函式、圓、勻速動點問題、摺疊與旋轉。壓軸題是國中數學學習的難點,也是學生學習數學過程中的痛點。本...
四、以代數轉化為手段 第13講 線段和的最值 一、將軍飲馬型 二、費馬點型 三、胡不歸型 第14講 摺疊問題 一、翻折與幾何基本圖形 二、翻折與隱形圓 三、翻折與參數 第15講 尺規作圖 一、基本作圖 二、性質作圖 三、條件作圖 四、複雜作圖 第16講 定值 一、參數之定 二、幾何之定 參考答案 ...
《且思且行——國中數學教學探索》是2021年華中科技大學出版社出版的圖書。內容簡介 本書主要內容為國中數學教學及研究,包括教法學法研究;課本問題拓展;思想方法教學;試題靚點賞析;命題規律研究;競賽解題指導;初等數學研究;銜接教學研究等,適合國中數學師生及數學愛好者閱讀。本書匯聚作者近30年的國中數學教學經驗...
分冊,重點從空間與平面、動與靜的視角研究立體幾何中的截面問題及摺疊展開等動態問題以及幾何體與球切接的模型;在機率統計常用模型的基礎上轉化演繹出各樣計算、計數、決策等問題.豐富的方法和技巧貫穿始末,精彩紛呈.本書適合數學成績優秀的學生挑戰高分甚至滿分使用,也適合高中數學教師、高考數學研究者,以及廣大數學...
《沿圓錐體側面的最短路徑問題》是伊金霍洛旗四中學校提供的微課課程,主講教師為徐曉梅 。課程簡介 人教版義務教育課程標準實驗教科書九年級上冊 第24章 圓 《24.4——弧長和扇形面積》微教學設計 新課標指出:”數學教育不僅要使學生獲得數學知識,用數學知識去解決實際問題,而且更重要的是:使學生認識到,數學就...
“數學精確了,怎么會說謊?”妞妞眼睛瞪大,一副難以置信的樣子。三、找規律 數學家會根據已經發生的事情,建立模型來預測未來的事情。四、邏輯的力量 如果問兩個武士中任何一個人如下問題“如果我問另外一位武士哪道門是自由之門,他會指向哪道門?”會怎么樣?五、合作才好 別的財產都好辦,就是家裡的17匹...
12.2偉大的數學家——歐拉 第13章美麗的球體 13.1球的體積與表面積公式的推導 13.2球面距離 第14章摺疊 14.1摺疊問題(一)14.2摺疊問題(二)圓錐曲線篇 第15章曲線系 15.1曲線與方程 15.2直線系 15.3圓系 15.4圓錐曲線系 第16章圓錐曲線的統一定義 16.1橢圓的第二定義 16.2雙曲線的第二定義 1...
《國中數學平面幾何30講》是2019年浙江大學出版社出版的圖書,作者是應佳成、李馨。內容簡介 德國著名數學家希爾伯特(Hilbert,1862-1943)在1900年巴黎第二屆國際數學家大會上的著名講演中提到:“在解決一個數學問題時,如果我們沒有獲得成功,原因常常在於我們沒有認識到更一般的觀點,從這種觀點來看,眼下要解決的...
1.直線與平面的位置關係 A組 B組 C組 2.簡單幾何體 A組 B組 C組 3.空間向量及其運算 A組 B組 C組 4.空間中的距離和角 A組 B組 C組 5.幾何體的面積和體積 A組 B組 C組 6.截面問題 A組 B組 C組 7.摺疊、旋轉、展開 A組 B組 C組 8.立體幾何綜合題 A組 B組 C組 參考答案 ...
七 用方程解決問題 第1課時 郵票的張數 第2課時 相遇問題 第3課時 練習六(1)第4課時 練習六(2)數學好玩 第1課時 “象徵性”長跑 第2課時 有趣的摺疊 第3課時 包裝的學問 八 數據的表示和分析 第1課時 複式條形統計圖 第2課時 複式折線統計圖(1)第3課時 複式折線統計圖(2)第4課時 平均數的...
1生活中的立體圖形 2展開與摺疊 3截一個幾何體 4從三個方向看物體的形狀 中考熱點問題聚焦 第二章有理數及其運算 1有理數 2數軸 3絕對值 4有理數的加法 5有理數的減法 6有理數的加減混合運算 7有理數的乘法 8有理數的除法 9有理數的乘方 10科學記數法 11有理數的混合運算 ……
7.3 平行四邊形中的摺疊問題 7.4 三角形中位線問題 7.5 平行四邊形中的面積問題 7.6 平行四邊形中的綜合問題 第8章 圖形變換 8.1 利用平移構造平行四邊形 8.2 利用倍半關係構造軸對稱圖形 8.3 利用軸對稱探究幾何最值問題 8.4 利用旋轉性質探究圖形中的不變數 8.5 利用線段中點構造中心對稱圖形 8....
《圓柱體沿異面爬行的最短路程問題》是伊金霍洛旗四中學校提供的微課課程,主講教師為徐曉梅 。課程簡介 《勾股定理的套用——圓柱體異面爬行》微教學設計 新課標指出:”數學教育不僅要使學生獲得數學知識,用數學知識去解決實際問題,而且更重要的是:使學生認識到,數學就在我們身邊。”本節課正是體現“生活數學化,...
題型66數學建模——周期現象描述 第四節解三角形 題型67正弦定理及其套用 題型68餘弦定理及其套用 題型69面積公式的套用 題型70射影定理的套用 題型71解三角形的綜合問題 題型72解三角形在測量工作中的套用 第五章平 面 向 量第一節平面向量的概念及線性運算 題型73平面向量的概念辨析 題型74平面向量的線性運算 ...
112.摺疊問題巧解決 113.六艘汽船 114.河寬多少 115.最好的類比 116.哪個影子大 117.潮水和繩梯 118.巧切正四面體 119.不規則形狀的玻璃瓶 120.山谷 121.拜訪好友 122.砝碼 123.最後剩下誰 124.下一個字母 125.分辨圓木根梢 126.巧妙過橋 127.火車過橋 第二章認知思維 1.量水的學問 2.奇怪的鉛球 3....
公元前7世紀,古希臘科學家、哲學家泰勒斯就對球的面積、體積、與長度等問題的研究就含有微積分思想。公元前3世紀,古希臘的數學家、力學家阿基米德(公元前287年~公元前212年)的著作《圓的測量》和《論球與圓柱》中就已含有積分學的萌芽,他在研究解決拋物線下的弓形面積、球和球冠面積、螺線下的面積和旋轉雙...
題49 摺疊問題圓錐模型 小結3 方法與升華 主題四 統計與機率 第九章 統計 9.1 隨機抽樣 題50 抽樣方法機率相同 題51 差異明顯分層抽樣 9.2 用樣本估計總體 題52 作直方圖估計總體 題53 集中趨勢三特徵數 題54 離散程度方(標準)差 小結4 方法與升華 第十章 機率 10.1 隨機事件與機率 題55 古典概型選...
數學問題是數學教學改革的風向標,當新的數學課程標準在全國實行之後,數學中考題型變得多彩,呈現出百花齊放的局面。本書在編寫過程中,編者不但要求題型新穎,對所有題目的難度層次、知識含量和題目質量也有非常嚴格的把握,堅持一個宗旨,即保證學生做每一道題都能有所得。作品目錄 一、創新型填空題 1.多選填空題 2...
勾股定理現約有500種證明方法,是數學定理中證明方法最多的定理之一。勾股定理是人類早期發現並證明的重要數學定理之一,用代數思想解決幾何問題的最重要的工具之一,也是數形結合的紐帶之一。在中國,周朝時期的商高提出了“勾三股四弦五”的勾股定理的特例。在西方,最早提出並證明此定理的為公元前6世紀古希臘的畢達...
(由於格式問題,推導過程見右圖1)此過程由“段”提供 實驗驗證 取一張正方形紙,15cm*15cm為宜,按上述步驟摺疊,取G點,將DC過G點沿AD邊向上翻折,得到摺痕①將AB向G點沿AD邊向下翻折,得到摺痕②,兩條摺痕將正方形紙3等分,適用範圍 1.折分數 2.折任意精度的角度 理論推廣 一般化1(C'為中點→C;...
已知等邊三角形紙片ABC的邊長為8,D為AB邊上的點,過點D作DG//BC交AC於點G,DE⊥BC於點E,過點G作GF⊥BC於點F,把三角形紙片ABC分別沿DG、DE、GF按圖1所示方式摺疊,點A、B、C分別落在點A′、B′、C′處,若A′、B′、C′在距形DEFG內或其邊上,且互不重合,此時我們稱△A′B′C′(即圖...
例如:摺疊問題中摺疊前後圖形全等是解決問題的關鍵。2、狠抓重點內容,適當練習熱點題型。多年來,國中數學的“方程”、“函式”、“直線型”一直是中考重點內容。“方程思想”、“函式思想”貫穿於試卷始終。另外,“開放題”、“探索題”、 “閱讀理解題”、“方案設計”、“動手操作”等問題也是近幾年中考的熱點...
他是摺紙的復興者。他的作品很特別,將藝術與數學結合起來。他的標誌是高度仿真,很有生命氣息。(美國摺紙協會的簡·波利什 評)他最不尋常的一點是,對紙的直覺和摺紙時的技術敏感度。面對問題,他經常能看到解決辦法,並拿出一張紙來證明。(麻省理工副教授埃里克·戴梅納 評)羅伯特·朗的摺紙理論可以套用於...
求有關最小值問題,經常利用對稱的思想轉移點的位置,改變思維角度,再利用(直線)一次函式的解析式求得最小值點的坐標,真正體現出“數形結合”的數學思想。 [4] 圖3 例1 已知兩點A(0,2),B(4,1),點P是x軸上的一點,且PA+PB的值最小,求點P的坐標。
立體圖形中畫最短路徑的方法: 1.將立體圖形中螞蟻爬行的折面展成平面圖形; 2.在平面內連線AB; 3.還原成為立體圖形 設計意圖:從生活中問題出發,喚起學習興趣及探索欲望.圖文並茂,直觀生動,同時也激發好奇心。 (三)思維導圖 設計意圖:在系統的數學學習中通過體驗、認識與內化等過程,逐步形成相對穩定的思...
四邊形不具有三角形的穩定性,易於變形。但正是由於四邊形不穩定具有的活動性,使其在生活中有廣泛的套用,如拉伸門等拉伸、摺疊結構。平行四邊形 定義 兩組對邊分別平行的四邊形叫做平行四邊形(parallelogram)。性質 (1)如果一個四邊形是平行四邊形,那么這個四邊形的兩組對邊分別相等。(簡述為“平行四邊形的兩...
