摺紙數學指的是對摺紙藝術從數學的角度加以研究。例如,研究某個特定的紙模型的可展性以及使用摺紙來解數學方程。
基本介紹
- 中文名:摺紙數學
- 定義:對摺紙藝術從數學的角度加以研究
- 研究成果:Huzita-Hatori 公理集
- 算法:《幾何摺紙算法》
定義
解釋
簡述
摺紙算法
套用
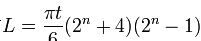 圖示
圖示摺紙數學指的是對摺紙藝術從數學的角度加以研究。例如,研究某個特定的紙模型的可展性以及使用摺紙來解數學方程。
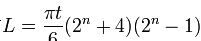 圖示
圖示摺紙數學指的是對摺紙藝術從數學的角度加以研究。例如,研究某個特定的紙模型的可展性以及使用摺紙來解數學方程。...
《摺紙與數學》是2012年科學出版社出版的圖書,作者是黃燕苹、李秉彝。本書主要介紹了摺紙幾何學的基本公理、操作過程以及基本性質。...
摺紙幾何學,又稱作摺紙數理學,指的是對摺紙藝術從數學的角度加以研究。例如,研究某個特定的紙模型的可展性以及使用摺紙來解數學方程。從19世紀開始,摺紙在西方...
摺紙是一種以紙張折成各種不同形狀的藝術活動。摺紙不只限於使用紙張。世界各地的摺紙愛好者在堅持摺疊規範的同時,使用了各種各樣的材料,如:錫箔紙、餐巾紙、醋酸...
摺紙藝術起源於中國。摺紙藝術是用一張完整的紙用摺疊的方法而成就的各種人物、動物或草木的形態的方法。...
摺紙是一種以紙張折成各種不同形狀的藝術活動。摺紙不只限於使用紙張。世界各地的摺紙愛好者在堅持摺疊規範的同時,使用了各種各樣的材料,如:錫箔紙、餐巾紙、醋酸...
《數學名題》中國大百科全書出版社出版,作者李延林。...... 數學名題作品目錄 編輯 目錄 猴子分桃問題 蟲蝕算問題 別內基托夫問題 黑洞數問題 世界末日問題 摺紙...
《每課一練數學》是2007年北京出版社出版集團,北京出版社出版的圖書。本書與課堂教學同步、與教材題量相當,題型新、題目精,對學生進行科學有效的訓練,使學生在學習...
《數學與藝術》是2007年上海教育出版社出版的圖書,作者是伊凡斯﹒彼得生。本書深入淺出地介紹了許多數學與藝術相結合的內容,通過兩百多幅插圖、二十幾幅彩圖介紹...
數學的奧秘圖書目錄 編輯 一 奇妙的問題 1.蘋果和籃子 2.到度有幾隻貓 ...七 摺紙的問題 八 圖形的魔術 九 猜數字遊戲 十 更有趣的遊戲 十一 ...
《數學王國中的未解難題》是一部數學書籍。《數學王國中的未解難題》是一本融科學性、趣味性、知識性於一體的科普類圖書,收錄了一些數學王國中至今仍還沒有得到...
《數學的奧妙》是2007年北京燕山出版社出版的圖書,作者是(俄)伊庫納契夫。...... 《數學的奧妙》是2007年北京燕山出版社...七、摺紙的問題八、圖形的魔術九、猜...
《發現數學原來數學這么有趣》是2008年4月1日電子工業出版社出版的圖書,作者是帕帕斯。...
摺紙對培養孩子的智慧和動手能力大有好處:首先,在折的過程中,孩子需要調動手、腦、眼三種感官,對培養孩子的觀察、想像和創造的能力有積極作用;其次,各種形狀和圖案...
真沒想到,小小的卷象竟然會玩高明的摺紙遊戲,真是種神奇的蟲子啊。卷象為什麼...由於家貧,法布爾沒能讀完中學,但是通過勤奮自學,他先後取得了數學學士學位、物理...
“挑戰最強大腦”系列,是為小學生量身打造的一套有趣的知識讀物,分別為“數學小魔術”“成語接龍”“填字遊戲”,隨時隨地可以放手玩,對於拓展學生的知識面來說,...
《數學小百科(數學常識):千千萬與萬萬千》通過有趣的數學遊戲來提高小學生學習數學的主動性和積極性。數學知識不是枯燥無味的,數學中充滿了無窮的樂趣,只要善於...
趣多多立體剪摺紙 作者:王雲、顧莉英 著叢書名:出版日期:2018年9月書號:978-7-122-32373-6開本:B5 710×1000 1/16裝幀:平版次:1版1次頁數:194頁《趣多多...
《愛上數學:10以內的運算》在開始練習之前,通過繪畫、找出藏著的物品等遊戲,初次接觸數學概念,閱讀數學童話,理解數學概念後再做相應的練習,使學過的知識爛熟於心...
《數學教師教育》共分為六章(第一章:課程標準;第二章:教學類別;第三章:教學研究;第四章:教學藝術;第五章:教學設計;第六章:教學案例)。每章又分門別類地...
《國小數學文化叢書:藝術與數學》為小朋友們精心選取了數學與藝術結合的20顆明珠,將它們寫成為一個個趣味、智慧的連環畫故事,讓你在緊張的學習之餘,和故事主人翁...
