惟一分解定理有多種指代意義,一個是指整數惟一分解定理,即算術基本定理,也可以指多項式的惟一分解定理,是多項式理論的主要命題之一,還可以指交的惟一分解定理,它是交換諾特環理論的基本定理,也是理想論的核心,也指乘積的惟一分解定理,它是交的惟一分解定理在有單位元的諾特環中的套用。
基本介紹
- 中文名:惟一分解定理
- 外文名:unique decomposition theorem
- 所屬學科:數學
- 簡介:整數、多項式、交的惟一分解定理
整數惟一分解定理
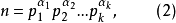
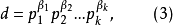
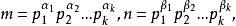
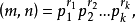
多項式的惟一分解定理
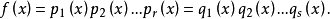
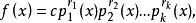
交的惟一分解定理
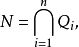
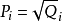
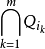
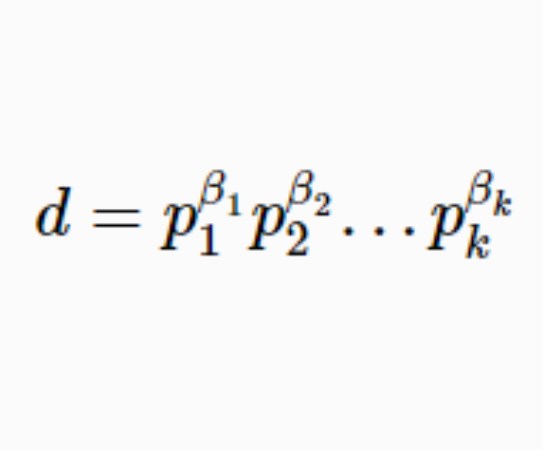
惟一分解定理有多種指代意義,一個是指整數惟一分解定理,即算術基本定理,也可以指多項式的惟一分解定理,是多項式理論的主要命題之一,還可以指交的惟一分解定理,它是交換諾特環理論的基本定理,也是理想論的核心,也指乘積的惟一分解定理,它是交的惟一分解定理在有單位元的諾特環中的套用。
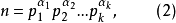
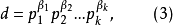
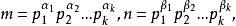
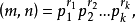
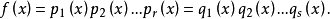
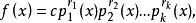
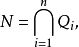
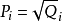
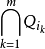
惟一分解定理有多種指代意義,一個是指整數惟一分解定理,即算術基本定理,也可以指多項式的惟一分解定理,是多項式理論的主要命題之一,還可以指交的惟一分解定理,它是...
算術基本定理可表述為:任何一個大於1的自然數 N,如果N不為質數,那么N可以唯一分解成有限個質數的乘積N=P1a1P2a2P3a3...Pnan,這裡P1<P2<P3...<...
霍奇分解定理是一個由數學家霍奇提出的關於微分p形式空間問題的定理,是微分p形式空間可以分解為其被運算元作用的像集與調和p形式空間的直和的定理。...
勒貝格分解定理(Lebesgue decomposition theorem)是關於σ有限廣義測度分解為絕對連續部分和奇異部分之和的重要定理,是有界變差函式的勒貝格分解定理的推廣。設(Ω,F,...
分式分解定理(principle of decomposition of afraction)分式的一種恆等變形.關於一個一元真分式總可以按其分母的因式化成若干一元真分式的和。...
黎曼對稱空IH}的分解定理(decomposition the-orems of Riemannian symmetric spaces)刻畫黎曼對稱空間的基本定理.第一分解定理。...
埃爾米特對稱空lad的分解定理(decompositiontheorems of Hermitian symmetric spaces)刻畫埃爾米特對稱空間的基本定理.第一個分解定理:單連通埃爾米特對稱空間可惟一地分解...
空間向量分解定理是指如果三個向量a,b,c不共面,那么對空間任一向量p,存在一個唯一的有序實數組x,y,z,使p=xa+yb+zc。表達式xa+yb+zc叫做向量a,b,c的...
1 定理 2 證明 3 例子 每個次數不小於1的實係數多項式在實數域上都可以唯一的分解成一次因式與二次不可約因式的乘積。 [1] 因此實係數多項式的根要么為實...
復係數多項式因式分解定理:每個次數大於等於1的復係數多項式在複數域上都可以唯一地分解成一次因式的乘積。...
