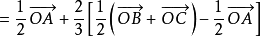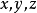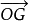空間向量分解定理是指如果三個向量a,b,c不共面,那么對空間任一向量p,存在一個唯一的有序實數組x,y,z,使p=xa+yb+zc。表達式xa+yb+zc叫做向量a,b,c的線性表達式或線性組合。
基本介紹
- 中文名:空間向量分解定理
- 外文名:Space vector decomposition theorem
- 所屬學科:數學
- 相關概念:線性表達式、線性組合、向量等
定理,定理的證明,推論,例題,
定理

定理的證明
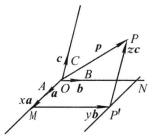 圖1
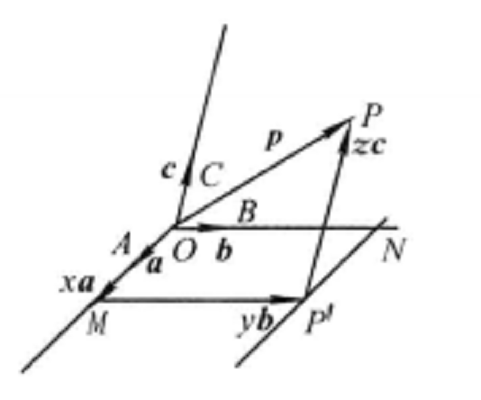
圖1設 不共面(圖1),過點O作
不共面(圖1),過點O作 ,過點P作直線PP'平行於OC,交平面OAB於點P',在平面OAB內,過P'作直線
,過點P作直線PP'平行於OC,交平面OAB於點P',在平面OAB內,過P'作直線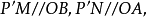 分別與直線OA,OB相交於點M,N,於是存在三個實數x,y,z,使
分別與直線OA,OB相交於點M,N,於是存在三個實數x,y,z,使


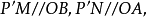
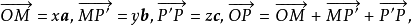


令 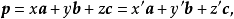
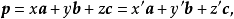
由於 不共面,可推出
不共面,可推出


由上述定理可知,如果三個向量 是不共面的向量(線性無關),那么
是不共面的向量(線性無關),那么 的線性組合
的線性組合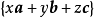 能生成所有的空間向量,這時
能生成所有的空間向量,這時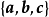 叫做空間的一個基底,其中
叫做空間的一個基底,其中 都叫做基向量。同時可知,空間任意三個不共面的向量都可構成空間的一個基底。
都叫做基向量。同時可知,空間任意三個不共面的向量都可構成空間的一個基底。


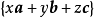
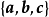

( )式叫做向量p的沿基向量的分解式。
)式叫做向量p的沿基向量的分解式。

如果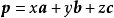 ,那么(x,y,z)叫做向量p關於
,那么(x,y,z)叫做向量p關於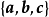 的坐標。
的坐標。
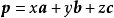
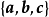
推論
設O,A,B,C是不共面的四點,則對空間任一點P,都存在唯一的三個有序實數x,y,z,使

例題
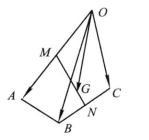 圖2
圖2解: 由線段中點的向量表達式,得