基本介紹
- 中文名:希臘幾何三大問題
- 所屬地區:希臘
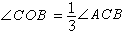

希臘幾何三大問題,數學術語,古希臘幾何作圖的三大問題是:①化圓為方,求作一正方形,使其面積等於一已知圓;②三等分任意角;③倍立方,求作一立方體,使其體積是一已知立方體的兩倍。這些問題的難處,是作圖只許用直尺(沒有刻度,只...
幾何三大問題(Three major geometric problems),亦稱尺規作圖問題,源於古希臘是幾何學中的著名問題,主要包括尺規作圖三大問題:(1)三等分角問題:即把任意一個已知角三等分;(2)立方倍積問題:即求作一個立方體,使它的體積等於已知立方體的體積的2倍;(3)化圓為方問題:也稱圓積問題,即求作一個正方形...
這其中最著名的是被稱為幾何三大問題的古典難題:三等分角問題:三等分一個任意角;倍立方問題:作一個立方體,使它的體積是已知立方體的體積的兩倍;化圓為方問題:作一個正方形,使它的面積等於已知圓的面積。在2400年前的古希臘已提出這些問題,直至1837年,法國數學家萬芝爾才首先證明“三等分角”和“倍立方...
解的尺規作圖問題。根據尺規作圖準則,該方程之解無法作出,因此,立方倍積問題和三等分角問題、化圓為方問題一起,成為古希臘三大幾何難題。立方倍積問題不能用尺規作圖方法解決的嚴格證明是法國數學家萬采爾(P.-L. Wantzel,1814-1848)於1837年給出的。立方倍積問題也叫第羅斯問題,傳說愛琴海中第羅斯(Delos)...
倍立方體問題(problem of duplication of a cube )是二千四百年前古希臘人提出的幾何三大作圖問題之一 。假設已知立方體的棱長是1個單位,那么這個立方體的體積便是1的3次方等於1。根據需求,要求作的立方體的體積是原立方體的兩倍,即1×2=2,...簡介 2倍立方體問題(problem of duplication of a cube )是二...
埃利亞學派的芝諾(Zeno)提出四個著名的悖論(二分說、追龜說、飛箭靜止說、運動場問題),迫使哲學家和數學家深入思考無窮的問題。智人學派提出幾何作圖的三大問題:化圓為方、倍立方體、三等分任意角。希臘人的興趣在於從理論上去解決這些問題,是幾何學從實際套用向演繹體系靠攏的又一步。正因為三大問題不能用標尺...
幾何是研究空間結構及性質的一門學科。它是數學中最基本的研究內容之一,與分析、代數等等具有同樣重要的地位,並且關係極為密切。 名稱由來 幾何藝術幾何一詞最早起源於希臘語“γεωμετρία”,由“γέα”(土地)和“μετρεĭν”(測量)兩個詞合成而來,指土地的測量,即測地術。後來轉化為拉丁...
2.1 笛卡兒和他的“眼鏡”——解析幾何的創立 2.2 捷運與公共汽車——解析法與綜合法的比較 習題4 2.3 三等分角問題——希臘幾何三大問題不能用尺規作圖的證明 習題5 3.解題技巧舉例 3.1 輪換及分比 習題6 3.2 斜角坐標系的優勢 習題7 3.3 旋轉與複數 習顥8 3.4 反用解析幾何——用解析幾何方法...
2.1 笛卡兒和他的“眼鏡”——解析幾何的創立 2.2 捷運與公共汽車——解析法與綜合法的比較 習題4 2.3 三等分角問題——希臘幾何三大問題不能用尺規作圖的證明 習題5 3.解題技巧舉例 3.1 輪換及分比 習題6 3.2 斜角坐標系的優勢 習題7 3.3 旋轉與複數 習顥8 3.4 反用解析幾何——用解析...
本書適合對此感興趣的大學生,中學教師,以及有較好代數和幾何基礎的中學生等閱讀。目錄 叢書序 序言 第Ⅰ章 古希臘的成就 第Ⅱ章 可作圖性的解析準則 第Ⅲ章 複數 第Ⅳ章 提洛問題 第Ⅴ章 三等分角的問題 第Ⅵ章 化圓為方問題 第Ⅶ章 正多邊形的作圖問題 第Ⅷ章 最後的評述 建議進一步閱讀的圖書 更高深...
用直尺和圓規三等分任意角的幾何作圖法 《用直尺和圓規三等分任意角的幾何作圖法》是2010年5月5日武漢出版社出版的圖書,作者是彭林章。內容介紹 該文研究的是古希臘三大幾何作圖問題之一,即用直尺和圓規進行有限次作圖,講任意角三等分的幾何作圖法。
在數學上,他們提出“三大問題”:①三等分任意角;②倍立方,求作一立方體,使其體積是已知立方體的二倍;③化圓為方,求作一正方形,使其面積等於一已知圓。問題的難處,是作圖只許用直尺(沒有刻度的尺)和圓規。希臘人的興趣並不在於圖形的實際作出,而是在尺規的限制下從理論上去解決這些問題。這是幾何學從...
1.代數數和超越數的定義 2.代數數按高度的排列 3.超越數存在性的證明 第二章關於兀的計算和作圖的歷史概觀 1.經驗時期 2.希臘數學家 3.從1670年到1770年的現代分析 4,5.1770年起評論嚴格性的復興 第三章數e的超越性 第四章數兀的超越性 第五章積分儀與兀的幾何作圖 ...
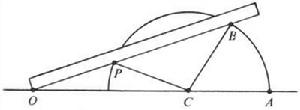
三等分角問題是希臘三大幾何作圖問題之一,即僅用直尺與圓規是否可以三等分任意角。限定直尺只能過一點或兩點畫直線,圓規只能在已知圓心、半徑時畫圓。1837年,法國數學家旺策爾(P.-L.Wantzel)證明了可尺規作圖的量必須滿足一個2次的方程,進而推出:在一般情況下,尺規三等分任一角是不可能的.這裡的結論是有一定...
尺規作圖三等分角是在公元前五世紀由古希臘人提出來的難題,該命題已經被數學家伽羅瓦用《近世代數》和《群論》證明是不可能的。概念來源 三等分角大約是在公元前五世紀由古希臘人提出來的,它和“立方倍積問題”、“化圓為方問題”一起被稱為“古代三大幾何難題”。 兩千多年來,從初學幾何的青少年到經驗豐富...
由於對尺規作圖的限制,使得一些貌似簡單的幾何作圖問題無法解決。最著名的是被稱為幾何三大問題的三個古希臘古典作圖難題:立方倍積問題、三等分任意角問題和化圓為方問題。當時很多有名的希臘數學家,都曾著力於研究這三大問題,雖然藉助於其他工具或曲線,這三大難題都可以解決,但由於尺規作圖的限制,卻一直未能...
古今以來,一些特意提出的數學難題有:平面幾何三大難題、希爾伯特的23個問題、世界三大數學猜想、千禧年大獎難題等。三大數學猜想 費爾馬大定理 費爾馬大定理起源於三百多年前,挑戰人類3個世紀,多次震驚全世界,耗盡人類眾多最傑出大腦的精力,也讓千千萬萬業餘者痴迷。終於在1994年被安德魯·懷爾斯攻克。古希臘數學家...
幾何學的發展從歐幾里得幾何的一統天下發展到各種非歐幾何學也是如此。在十九世紀發現了許多用傳統方法不能解決的問題,如五次及五次以上代數方程不能通過加、減、乘、除、乘方、開方求出根來;古希臘幾何三大問題,即三等分任意角、倍立方體、化圓為方不能通過圓規、直尺作圖來解決等等。這些否定的結果表明了傳統...
三等分角是古希臘平面幾何里尺規作圖領域中的著名問題,與化圓為方及倍立方問題並列為尺規作圖三大難題。尺規作圖是古希臘人的數學研究課題之一,是對具體的直尺和圓規畫圖可能性的抽象化,研究是否能用規定的作圖法在有限步內達到給定的目標。三等分角問題的內容是:“能否僅用尺規作圖法將任意角度三等分?”三...
安蒂豐就這樣認為自己解決了希臘幾何作圖的三大問題之一一化圓為方。當然,安蒂豐沒有成功是明顯的,可我們從這裡得到的信息卻是模糊的,推測他是受了德謨克利特原子論學派的影響。另外, 所謂“相合一致” 是極為素樸的直覺觀念。事實上, 在此過程中, 多邊形永遠不能與圓相合。無論如何, 這種不斷作內接正...
文藝復興時期,義大利著名藝術大師達·文西(1452~1519)為化圓為方問題所吸引,並獲巧妙方法。如圖3,設圓半徑為R,以圓為底作高為R/2的圓柱,然後將圓柱在平面上滾動一周,得矩形。將矩形化方,即完成化圓為方。以上我們看到,希臘人很早就意識到(但未能證明)三大難題不能以尺規在有限步驟內完成。但它們...
幾何學的發展從歐幾里得幾何的一統天下發展到各種非歐幾何學也是如此。在十九世紀發現了許多用傳統方法不能解決的問題,如五次及五次以上代數方程不能通過加、減、乘、除、乘方、開方求出根來;古希臘幾何三大問題,即三等分任意角、倍立方體、化圓為方不能通過圓規、直尺作圖來解決等等。這些否定的結果表明了傳統...
第3章 三等分角尺規作圖問題的解決 3.1 作圖問題的代數化 3.2 作實數的和、差、積、商及平方根 3.3 尺規作圖能作哪些新的實數 3.4 整係數代數方程的有理根 3.5 通過開平方擴充數域 3.6 一元n次方程根與係數的關係 3.7 三等分角尺規作圖問題的解決 第4章 古希臘三大作圖問題 第5章 等分...
尺規作圖歷史悠久,影響深遠,特別是古希臘三大幾何難題更是吸引了無數數學愛好者,尺規作圖看似簡單,其實奧妙無窮,具有挑戰性,能夠培養數學思維和數學能力。隨著人們數學水平的提高,從最開始的尺規作圖,又引發出了單規作圖、單尺作圖等更高難度的作圖。下面介紹單尺作圖的幾個實例,並用面積法給出證明。【例1...
古代三大幾何難題其中之一,便是化圓為方。這個起源於古希臘的幾何作圖題,在2000多年裡,不知難倒了多少能人,直到19世紀,人們才證明了這個幾何題,是根本不可能用古代人的尺規作圖法作出來的。古代數學家的貢獻 中國古代的數學家祖沖之,從圓內接正六邊形入手,讓邊數成倍增加,用圓內接正多邊形的面積去逼近圓...
約公元前460年,希臘智人學派提出幾何作圖三大問題:化圓為方、三等分角和二倍立方 約公元前460年 - 前401年:古希臘歷史學家修昔底德在世,著有《伯羅奔尼撒戰爭史》。約公元前460 - 前370年:古希臘哲學家德謨克利特在世。公元前460~前370年:古希臘科學家希波克拉底等人建立希臘醫學並提出健康與病態理論...
判別準則I:給定複數域C中元z,若F=Q,Q是有理數域,則z可利用尺規表示的充分必要條件是,z屬於C的一個子域K=F(u,)中,其中K是F的平方根塔.由判別準則工,所謂古希臘幾何三大問題不能用尺規作出. 判別準則亞:複數z可由複數z用尺規作出的充分必要條件是,z為F=Q, ,上代數元,且F(z)/F的正規閉包在F上的...
早期對圓錐曲線進行系統研究成就最突出的可以說是古希臘數學家阿波羅尼(Apollonius,前262~前190)。他與歐幾里得是同時代人,其巨著《圓錐曲線》與歐幾里得的《幾何原本》同被譽為古代希臘幾何的登峰造極之作。在《圓錐曲線》中,阿波羅尼總結了前人(柏拉圖學派的梅內赫莫斯為解決倍立方體問題而發現了圓錐曲線)的工作...
