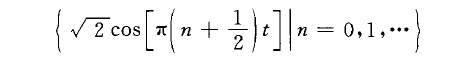
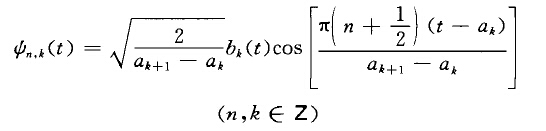
局部三角變換(local trigonometric transform)在處理語音信號中一類重要的變換。
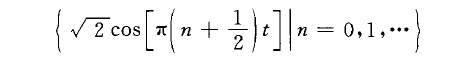
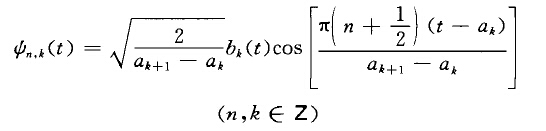
局部三角變換(local trigonometric transform)在處理語音信號中一類重要的變換。函式系形成L[0,1]的規範正交基.通過視窗函式的折摺變換可用它們構造Lz(R)的正交基.如果R= Uklk是一個...
設G為局部緊交換群，Ĝ為G的對偶群，線性映射𝓕:L²(G)→L(Ĝ)，f→𝓕f滿足普朗歇爾公式 且當f∈L¹(G)∩L²(G)時，𝓕f就是f的傅立葉變換f。對這樣的映射𝓕，稱𝓕f為f的普朗歇爾變換。傅立葉變換 傅立葉變換，表示能將滿足一定條件的某個函式表示成三角函式（正弦和/或餘弦函式）...
小波變換（wavelet transform，WT）是一種新的變換分析方法，它繼承和發展了短時傅立葉變換局部化的思想，同時又克服了視窗大小不隨頻率變化等缺點，能夠提供一個隨頻率改變的“時間-頻率”視窗，是進行信號時頻分析和處理的理想工具。它的主要特點是通過變換能夠充分突出問題某些方面的特徵，能對時間（空間）頻率的...
7.6 超完備表示、框架、冗餘變換和自適應基 108 7.6.1 超完備表示 108 7.6.2 矩陣的例子 109 7.6.3 平移不變冗餘小波變換和非抽取濾波器組 111 7.6.4 框架和基的自適應構造 112 7.7 局部三角函式基 113 7.7.1 非光滑局部三角函式基 114 7.7.2 光滑窗的構造 114 7.7.3 摺疊和伸展 116 7...
公式 (1)(sinα)^2+(cosα)^2=1 (2)1+(tanα)^2=(secα)^2 (3)1+(cotα)^2=(cscα)^2 證明下面兩式，只需將一式，左右同除(sinα)^2,第二個除(cosα)^2即可 (4)對於任意非直角三角形，總有 tanA+tanB+tanC=tanAtanBtanC 萬能公式 證明 整理可得 得證 同樣可以得證,當x+y+z=nπ...
楊輝三角，是二項式係數在三角形中的一種幾何排列，中國南宋數學家楊輝1261年所著的《詳解九章算法》一書中出現。在歐洲，帕斯卡（1623---1662）在1654年發現這一規律，所以這個表又叫做帕斯卡三角形。帕斯卡的發現比楊輝要遲393年，比賈憲遲600年。楊輝三角是中國數學史上的一個偉大成就。簡介 楊輝三角，是二項式系...
其逆變換為 直接使用DFT的定義計算的計算複雜度為 ，而快速傅立葉變換（fast Fourier transform, FFT）可以將複雜度改進為 。計算複雜度的降低以及數字電路計算能力的發展使得DFT成為在信號處理領域十分實用且重要的方法。在阿貝爾群上的統一描述 以上各種傅立葉變換可以被更統一的表述成任意局部緊緻的阿貝爾群上的...
1.2 角(值)關係視角下的恆等變換 2.幾何形態的三角函式 2.1 方程視角下的解三角形 2.1.1 代數條件下的解三角形 2.1.2 幾何條件下的解三角形 2.2 特殊邊角關係的解三角形 2.2.1 特殊邊(角)三角形 2.2.2 特殊邊角關係三角形 2.3 局部可解三角形 2.3.1 運動變化視角下解三角形 2.3.2 基本...
全局算法是指對整個物體模型或場景模型的簡化過程進行最佳化，而不僅僅根據局部的特徵來確定刪除不重要的元素。局部算法是指套用一組局部規則，僅考慮物體的某個局部區域的特徵對物體進行簡化。四、典型的LOD模型生成算法概述 1．近平面合併法 Hinkler等的幾何最佳化方法[3]檢測出共面或近似共面的三角面片，將這些三角面片...
將作用在單元上的外載荷同樣表示為局部坐標的函式，就可以在局部坐標下完成單元的載荷移置。體力移置的公式為：單元剛度矩陣 單元剛度矩陣表達式如下所示：稱為雅可比矩陣，由坐標變換式確定，當逆陣存在時，則形函式對x ，y 的導數可求，即應變陣可求。一般而言，等參單元的剛度積分很難有解析式，必須進行數值積分...
5.1 局部坐標變換 ……… 183 5.2 反饋精確線性化 ……… 190 5.3 非互動控制 ……… 202 5.4 擴展動態以獲得相對階 ……… 208 5.5 實例 ……… 220 5.6 輸入- 輸出回響精確線性化 ……… 232 第6 章 狀態反饋的幾何理論：工具… ………...
7.2.4 局部可解三角形 8.複數 8.1 複數的概念與幾何意義 8.2 複數的運算 9.立體幾何 9.1 空間幾何體的結構與度量 9.2 空間中的平行關係 9.3 空間中的垂直關係 9.4 空間向量的套用 9.4.1 空間向量與位置關係 9.4.2 空間向量與空間角 lO.平面解析幾何 10.1 直線方程 10.1.1 直線的幾何要素...
11.4 下三角形系統的鎮定 11.5 多輸入系統的設計 第12章 魯棒半全局穩定性的反饋設計 12.1 達到半全局實際穩定性 12.2 通過局部狀態反饋達到半全局鎮定 12.3 定理9.6.2的證明 12.4 下三角形最小相位系統的鎮定 12.5 不用分離原理通過輸出反饋鎮定 12.6 通過輸出反饋鎮定非最小相位系統 12.7 舉例 第...
較早的直接基於灰度圖像角點檢測是文獻提出的Kitchen?Rosenfeld算法,通過模板視窗局部梯度幅值和梯度方向的變換率來計算角點度量值C=I?xyI?2?y I?yyI?2?x-2I?xyI?xI?yI?2?x I?2?y,根據C與給定的閾值大小關係來判定該點是否是角點。Harris等人檢測方法考慮的是用一個高斯窗或矩形窗在圖像上移動,由模板視窗...
微課堂42 兩種配湊藉助三角 微課堂43 局部固定分解問題 微課堂44 消元思想化生為熟 微課堂45 觀察特點實現轉化 小結方法與升華7 高考熱點問題8 絕對值三角不等式 微課堂46 合理配湊運用結論 微課堂47 巧用特殊值建五不等式 微課堂48 猜想結論表示係數 微課堂49 最值互嵌回歸本質 微課堂50 代數推理幾何直觀 小結方法與...
（2）將所有的z向線段與工件模型上表面的交點按照一定的規則以三角形的形式連線構成的三角形格線面即可被視為工件模型的近似表示。2、 局部繪製技術 數控仿真過程中工件模型形狀特徵的改變僅在當前切削段的局部區域中，其他場景保持不變，如果僅對當前切削段局部區域進行局部繪製將會極大地減少參與消隱、光照和圖形生成...
f是常數。 對預序集合間的函式，常數函式是保序和倒序的；相反的，如果f既是保序的也是倒序的，如f的定義域是一個格，那么f一定是一個常數函式。常數函式的其他性質包括：任一定義域和陪域相同的常數函式是等冪的。 任一拓撲空間上的常數是連續的。 在一個連通集合中，若且唯若f是常數時，它是局部常數。
4.2三角變換 4.3三角函式 4.4平面解析幾何 4.4.1點 4.4.2直線與圓 4.4.3曲率與曲率半徑 4.4.4橢圓 4.4.5雙曲線 4.4.6拋物線 4.4.7擺線 4.4.8漸開線 4.4.9螺線 4.5空間解析幾何 4.5.1曲面及方程 4.5.2柱面及旋轉曲面 4.5.3二次曲面 4.6幾何要素分析 4.6.1直線—直線要素分析 ...
電網拓撲分析算法採用圖論與啟發式搜尋技術相結合的方法，通過修改母線的鄰接矩陣來快速跟蹤站內拓撲的變化，把母線重新分組並映射為電網的節點，然後採用啟發式搜尋算法搜尋電網的節點樹，快速跟蹤並更新發生變化的局部電網拓撲。根據已知的電網拓撲，啟動並行算法求取電網當前的節點阻抗陣和邊界等值，並把邊界等值傳送給...
8.3.1 局部處理方法 8.3.2 Hough變換及實現方法 8.4 閾值分割法 8.4.1 單閾值分割與多閾值分割 8.4.2 均值疊代閾值分割法 8.4.3 最大類間方差的分割法 8.4.4 常見的多閾值分割法 8.5 基於區域的分割方法 8.5.1 區域生長算法 8.5.2 區域分裂合併算法 8.6 基於能量的分割方法 8.6.1 主動...
拓撲變換 莫比烏斯帶是一種拓撲圖形，它們在圖形被彎曲、拉大、縮小或任意的變形下保持不變，只要在變形過程中不使原來不同的點重合為同一個點，又不產生新點。換句話說，這種變換的條件是：在原來圖形的點與變換了圖形的點之間存在著一一對應的關係，並且鄰近的點還是鄰近的點。這樣的變換叫做拓撲變換。拓撲有一個...
這個非常基本而重要的結果稱之為局部性原理。G.G.斯托克斯和 P.L.von賽德爾引進了函式項級數一致收斂性的概念以後，傅立葉級數的收斂問題進一步受到了人們的注意。H.E.海涅在1870年的一篇論文中指出，有界函式ƒ(x)可以唯一地表示為三角級數這一結論，通常採用的論證方法是不完備的，因為傅立葉級數未必一致收斂，...
其中，基於智慧型最佳化的算法能獲得較好匹配，並且有較高的可靠性，但是建模複雜，疊代時間長，需要專門的數字處理器，最佳化結果對初值依賴性較強，容易陷入局部最優。 而設計耦合電路法實際套用較多，主要通 過改變匹配網路的結構及參數值來進行阻抗匹配，但匹配精度稍差，適用範圍存在一定局限性。聲表濾波器的阻抗匹配 隨...
凸函式還有一個重要的性質：對於凸函式來說，局部最小值就是全局最小值。綜上所述，凸函式的主要性質有：1.若f為定義在凸集S上的凸函式，則對任意實數β≥0，函式βf也是定義在S上的凸函式;2.若f₁和f₂為定義在凸集S上的兩個凸函式，則其和f=f₁+f₂仍為定義在S上的凸函式;3.若f(i=1，...
三角點位於從核心點開始的第一個分叉點或者斷點，或者兩條紋路會聚處、孤立點、折轉處，或者指向這些奇異點。三角點提供了指紋紋路的計數跟蹤的開始之處。紋數，即模式區內指紋紋路的數量。在計算指紋的紋路時，一般先連線核心點和三角點，這條連線與指紋紋路相交的數量即可認為是指紋的紋數。局部特徵 局部特徵指紋...
6.1.4 局部截斷誤差253 6.2 龍格-庫塔方法254 6.3 線性多步法259 6.4 邊值問題的差分方法和打靶法簡介262 6.4.1 解線性方程邊值問題的差分方法262 6.4.2 打靶法264 6.5 套用案例265 6.5.1 無源元件的“瞬態伴隨模型”的建立265 6.5.2 磁流體發電通道的數值計算270 6.5.3 平面溫度場計算問題...
源波函式是指一系非正餘弦的二項式周期波超函式，它可以通過參數控制產生不同的周期性波。。。比如常數波，三角波，矩形波，激波 函式定義 1. a ,b c，t為正實數, k, r為實數，t為函式周期，其他為波形控制參數 函式定義如下 基波函式：波函式： 指數波函式 函式起源 函式的起源與複數的積函式, 它是對於...
置換是很多算法成功的根本，包括有局部定支點(partialpivoting)的運算繁重的高斯消去法(這裡的置換用來定支點)。但是它們很少明顯作為矩陣出現；它們的特殊形式允許更有限的表示，比如n個索引的列表。同樣的，使用Householder和Givens矩陣的算法典型的使用特殊方法的乘法和存儲。例如，Givens旋轉只影響它所乘的矩陣的兩行，...
此外，在嗅皮層-海馬系統中，內嗅皮層的以下解剖和功能特徵也支持這一理論模型：（1）內嗅皮層第Ⅱ層含有的星狀細胞（格線細胞） ，在 theta 波頻範圍內呈現出局部閾下膜電位振盪（intrinsic sub- threshold membrane potential oscillations）特徵；（2）內嗅皮層接受前下托的信息投射，獲得頭部朝向的信息。不同頭...
